Случайная матрица

Cтраница 3

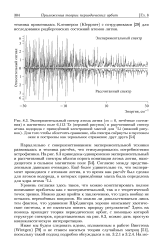
В процедуре обхода контура из близлежащих элементов-ячеек вокруг локальных центров переключения используется кодовая последовательность случайных матриц состояния, формирующихся на каждом временном шаге. При величине случайного числа, задаваемого датчиком случайных чисел, больше заданного критического значения Рсг порога переключения Р, имеет место переключение очередной соседней ячейки. Использование символической динамики состояния структуры позволяет устанавливать и сравнивать равновероятностный ( марковский) процесс разрастания областей переключения с аналогичным процессом при смещении срединной горизонтали распределения вероятностей ( квантиля), то есть с изменением уровня фильтрации значений датчика случайных чисел. [31]

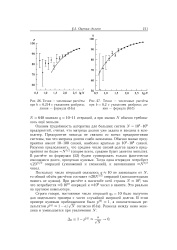Точки - численные расчеты [ IMAGE ] Точки - численные расчеты при b 0 214 с указанием разброса. при Ъ 0 2 с указанием разброса. ли-линия - формула ( 61 а ния - формула ( 616. [32]

Строго говоря, постоянное число итераций до 10 было получено для модельного примера с чисто случайной матрицей долгов. [33]

Заметим, что, в отличие от аналогичных выражений (2.131) и (2.132) для стационарной системы, квадратная случайная матрица СУ ( СУ) Т здесь не является статистически независимой и поэтому не может быть осреднена отдельно. [34]

В § 3 показано, что при га Inn 7п и п - оо вероятность примитивности случайной матрицы А имеет те же самые предельные выражения, что и вероятность неразложимости. Отсюда в качестве следствия получены предельные выражения для вероятности эргодичности однородной цепи Маркова для произвольного, вообще говоря, неподстановочного вероятностного преобразователя. [35]

Можно показать, что если п k - 1 и матрица S невырождена, то с вероятностью 1 случайная матрица V из ( 2) положительно определена. [36]

Эти формулы, однако, не настолько точны, чтобы с их помощью можно было вычислить другие важные характеристики случайных матриц. [37]

Применения этих понятий в теории динамических систем основываются на исглътипликативной эргодической теореме Оселедца [3], устанавливающей условия правильности произведений случайных матриц. Несмотря на многочисленность работ, посвященных показателям Ляпунова в различных ситуациях, судя по всему незамеченным до настоящего времени оставалось то простое обстоятельство, что правильность по Ляпунову последовательности - матриц равносильна ее асимптотической близости к последовательности степеней некоторой фиксированной матрицы. Это наблюдение дает возможность перенести классическую теорию характеристических показателей Ляпунова на произвольные некомпактные полупростые группы Ли с конечным центром, переформулировав ее в инвариантных геометрических терминах без использования матричных представлений этих групп. Применение аппарата римановой геометрии и теории симметрических пространств позволяет цроста получить как обобщения уже известных фактов, так и результаты, по-видимому не формулировавшиеся раньше и в матричной форме, в частности глобальный вариант закона больших чисел для полупростых групп Ли Наши доказательства являются новыми даже для матричных групп. [38]

Экспериментальный спектр атома лития ( т 0, нечетные состояния в магнитном поле 6 113 Тл ( верхний рисунок и рассчитанный спектр атома водорода с приведенной электронной массой для Li ( нижний рисунок. Для того чтобы облегчить сравнение, оба спектра свернуты в гауссовом окне и построены как зеркальное отражение друг друга. [39]

Ниже мы будем следовать идеям, изложенным в работе Винтгена ( Wintgen) [79] и не станем касаться теории случайных матриц [51], поскольку такой подход подробно обсуждался в пп. [40]

Отметим, что похожее, физически прозрачное представление было использовано Дайсоном ( Dyson, 1962) в теории спектральных корреляций случайных матриц, упомянутых в гл. Наименьшая энергия этой классической плазмы достигается, когда отрицательная плотность заряда 7П / ( 3, 2тг /) в точности компенсирует положительный заряд и обеспечивает зарядовую нейтральность. [41]

Стх определяется как линейное преобразование спектральной характеристики математического ожидания входного сигнала Сту детерминированным матричным оператором А, который представляет собой математическое ожидание случайной матрицы стохастического матричного оператора А. [42]

Соотношение ( 237) не предусматривает каких-либо ограничений на вероятностные характеристики входа, зато его практическое применение связано с определением вероятностных характеристик случайной матрицы весовых функций G ( t, т), что представляет определенные трудности. [43]

Поскольку квантовый спектр, как было установлено, однозначно связан с периодическими орбитами, которые в свою очередь зависят от индивидуальных характеристик системы, успех теории случайных матриц, единым образом описывающей спектральные корреляции любой хаотической системы, требует специального объяснения. [44]

В § 2 установлено, что если га lnn 7n, 7n - o ( lnn) и и - оо, то события, состоящие в неразложимости случайной матрицы А и отсутствии в этой матрице нулевых столбцов, в пределе имеют одну и ту же вероятность, которая равна е-е при jn - 7 и 1 при jn - оо. [45]

Страницы: 1 2 3 4