Преобразование есть

Cтраница 1

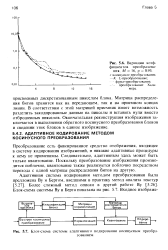Вариации коэффициентов преобразования, М 16, р. х косинусное преобразование. - К L-преобразование.| Блок-схема системы адаптивного кодирования косинусным преобразованием. [1]

Преобразование есть фиксированное средство отображения, входящее в систему кодирования изображений, и никакие адаптивные процедуры к нему не применимы. Следовательно, адаптивным здесь может быть только квантование. Поскольку преобразование изображения производится поблочно, квантование также реализуется поблочно посредством перехода с одной матрицы распределения битов на другую. [2]

Годографическое преобразование есть геометрическое представление динамических связей, которые существуют между векторными пространствами в ньютоновой механике. [3]

Унитарное преобразование есть преобразование от одной системы нормированных ортогональных ( унитарных) состояний к другой такой же системе. [4]

Любое ортогональное преобразование есть произведение поворота, параллельного переноса и, возможно, осевой симметрии. [5]

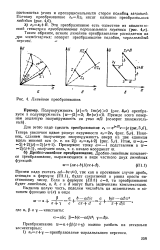Линейное преобразование. [6]

Это преобразование есть известное из аналити. [7]

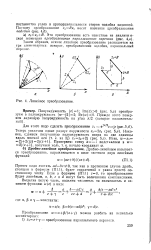Линейное преобразование. [8]

Это преобразование есть известное из аналитиге-ской геометрии преобразование параллельного переноса ( ряс. [9]

Каждое ортогональное преобразование есть произведение параллельного переноса, поворота и, возможно, отражения. [10]

Группа преобразований есть множество преобразований данного многообразия, которэе ( 1) содержит тождественное преобразование Е, ( 2) содержит для каждого преобразования S-обратное ему 5 - 1, и ( 3) вме-сте с каждой парой преобразований S T содержит их произведение ST. Пример: можно - определить конгруэнтные конфигурации в пространстве как множества точек, переходящие друг в друга при конгруэнтных преобразованиях npoqr - ранства. [11]

Всякое такое преобразование есть, очевидно, произведение гомотетии и переноса. [12]

Множество всех проективно-аффинных преобразований есть подгруппа группы всех проективных преобразований проективной плоскости, изоморфная группе аффинных преобразований аффинной плоскости. [13]

Так как второе преобразование есть просто параллельное перемещение пространства ( или плоскости) как целого и, стало быть, не вызывает никаких вопросов, то можно ограничиться исследованием одного лишь первого преобразования. [14]

Обратное к каждому элементарному преобразованию есть снова элементарное преобразование. Это легко проверяется для каждого из трех типов элементарных преобразований. [15]

Страницы: 1 2 3 4