Неустойчивость - равновесие
Cтраница 1
Неустойчивость равновесия между пересыщенным раствором или переохлажденным расплавом и кристаллом соответствующего радиуса выражается формальным образом в том, что термодинамический потенциал U образованной ими системы имеет при R R не минимальное значение, как при обычном устойчивом термодинамическом равновесии, а, наоборот, максимальное. [1]
Неустойчивость равновесия при растяжении компактных 2) образцов на пределе текучести. Предположим, что ц круглом стальном образце небольшая область имеет предел текучести более низкий, чем соседние части. Если бы эта область занимала свободное положение в пространстве, то при достижении предела текучести в ней появились бы пластические деформации растяжения порядка нескольких процентов в направлении действия растягивающих напряжений и деформации сжатия во всех поперечных направлениях, составляющие половину деформаций растяжения. [2]
Неустойчивость равновесия, вызывающая местное выпучивание в пластически деформированном цилиндре. Из экспериментов по пластическому деформированию длинных толстостенных цилиндров из пластичных металлов, подвергнутых действию высокого внутреннего давления, известно, что после достижения максимального давления процесс равномерного деформирования прекращается и цилиндр, прежде чем разрушиться, обнаруживает местное выпучивание. [3]
Неустойчивость равновесия между пересыщенным паром и жидкой каплей соответствующего радиуса г или между перегретой ( растянутой) жидкостью и пузырьком пара выражается формальным образом в том, что термодинамический потенциал Ф образованной ими системы имеет при гг не минимальное значение, как при обычном устойчивом термодинамическом равновесии, а, наоборот, максимальное. [4]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум. [5]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум, воспроизведенный в книге Общая задача об устойчивости движения, Москва - Ленинград, 1935, стр. [6]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум. [7]
О неустойчивости равновесия, когда силовая функция не есть максимум. [8]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть maximum. [9]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум. [10]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум / / Собр. [11]
О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум / / Прикл. [12]
Области неустойчивости равновесия для всех до ф О имеют конечную ширину. Однако, как показывают вычисления в следующих порядках, влияние вязкости приводит к их затуханию. Решения, построенные внутри областей неустойчивости, при всех до ф О экспоненциально нарастают. Таким образом, чтобы избежать нефизических, неограниченно возрастающих со временем решений, необходимо положить до - 0 - Наиболее опасной является первая резонансная зона, поскольку, как показано в § 1.1, обусловленный вязкостью порог возникновения резонанса для других зон лежит выше. [13]
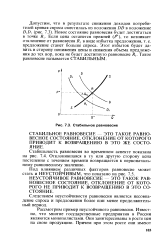 |
Стабильное равновесие. [14] |
Следствием неустойчивости равновесия является несовпадение спроса и предложения более или менее продолжительный период. [15]
Страницы: 1 2 3 4