Неустойчивость - равновесие
Cтраница 2
Вопросы неустойчивости равновесия возникают всюду, где имеются тонкостенные конструкции. Для тонкостенных же конструкций, изготовленных из слоистых пластиков вследствие малой жесткости последних, обеспечение устойчивости является особенно важной задачей при их проектировании. [16]
Это и означает неустойчивость равновесия. [17]
 |
Зависимость энергии Гиббса образования зародыша от его радиуса. [18] |
В критической точке неустойчивость равновесия проявляется в том, что существует равная вероятность возникновения и исчезновения зародышей конденсации. Если степень пересыщения больше критической величины, то возникающие зародыши будут самопроизвольно расти. Энергия Гпббса ( см. рис. 11.24) снижается с увеличением размеров зародышей от критического значения, отвечающего равновесию в соответствии с уравнением Кельвина. Образование новых зародышей прекращается. Данное состояние системы также является неустойчивым, так как в системе происходят постоянные процессы роста и исчезновения частиц дисперсной фазы: одна часть частиц растет за счет исчезновения другой части частиц. Более подробно этот процесс рассматривается в разделе об устойчивости дисперсных систем. [19]
В некоторых случаях установить неустойчивость равновесия можно на основании теорем Ляпунова. [20]
В некоторых случаях установить неустойчивость равновесия можно ла основании теорем Ляпунова. [21]
В некоторых случаях установить неустойчивость равновесия можно на основании теорем Ляпунова. [22]
В теоремах А. М. Ляпунова о неустойчивости равновесия рассмотрены практически важнейшие случаи обращения теоремы Лагранжа - Дирихле. [23]
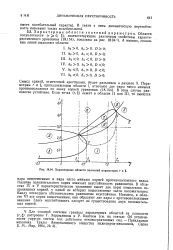 |
Характерные области значений параметров г a %. [24] |
Наличие положительного корня означает неустойчивость равновесия. В областях IV и V характеристическое уравнение имеет две пары комплексно сопряженных корней, у одной из которых вещественные части положительны. Ввиду последнего обстоятельства равновесие неустойчиво. Наконец, в области VI все корни вещественные; они образуют две пары с противоположными знаками. Здесь неустойчивость следует из существования двух положительных корней. [25]
В некоторых случаях установить неустойчивость равновесия можно на основании теорем Ляпунова. [26]
Они могут быть связаны с термоконвективной неустойчивостью равновесия облаков молекулярного газа в присутствии горячего тяготеющего центра. [27]
Конвективные движения в пористой среде вблизи порога неустойчивости равновесия / / Докл. [28]
Доказательство можно найти в работе: Ляпунов A.M. О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум / / Собр. [29]
Доказательство можно найти в работе: Ляпунов А. М. О неустойчивости равновесия в некоторых случаях, когда функция сил не есть максимум / / Собр. [30]
Страницы: 1 2 3 4