Нутация

Cтраница 2

Существованием нутации объясняется и другое поведение гироскопа, кажущееся парадоксальным. Согласно уравнению (49.3) момент импульса гироскопа L изменяется только тогда, когда на него действуют внешние силы. Если действие внешних сил прекращается, то мгновенно прекращается изменение вектора L, а с ним и прецессия гироскопа. Ось фигуры гироскопа становится неподвижной. Не противоречит ли закону инерции такая безынерционноспгъ оси фигуры гироскопа. Действительно, такое противоречие существовало бы, если бы указанная безынерцион-ность относилась к движению самой оси фигуры гироскопа. На самом деле эта безынерционность относится не к оси фигуры, а к вектору L. К выводу о безынерционное движения оси фигуры приводит приближенная теория гироскопа, пренебрегающая нутациями. Мы видим, таким образом, что учет нутаций устраняет противоречия с законом инерции. [16]

Третий-угол нутации д - лежит в плоскости гОг и его отсчитывают от оси Oz к оси Oz против хода часов, если смотреть с положительного направления линии узлов, а за положительное направление линии узлов принимают такое, глядя с которого 0 180, если отмеривать против хода часовой стрелки. [17]

Ось нутации при этом не перемещается, углы 8 и iji не изменяются, но вследствие вращения оси изменяется, очевидно, угол ср. Движение называют собственным вращением или ротацией, угол ср - углом собственного вращения или углом ротации, ось С - осью собственного вращения или осью ротации. [18]

Существованием нутаций объясняется и другое поведение гироскопа, кажущееся парадоксальным. Согласно уравнению (49.3) момент импульса гироскопа L изменяется только тогда, когда на него действуют внешние силы. Если действие внешних сил прекращается, то мгновенно прекращается изменение вектора L, а с ним и прецессия гироскопа. Ось фигуры гироскопа становится неподвижной. Не противоречит ли закону инерции такая безынерционность оси фигуры гироскопа. Действительно, такое противоречие существовало бы, если бы указанная безынерционность относилась к движению самой оси фигуры гироскопа. На самом деле эта безынерционность относится не к оси фигуры, а к вектору L. К выводу о безынерционное движения оси фигуры приводит приближенная теория гироскопа, пренебрегающая нутациями. Мы видим, таким образом, что учет нутаций устраняет противоречия с законом инерции. [19]

Амплитуда нутации зависит от причин ( начальных условий), которые ее вызвали. Но частота ее определяется только моментами инерции и угловой скоростью вращения вокруг оси симметрии. Тело может вращаться и без нутации, если его угловая скорость направлена строго по оси симметрии. К телам вращения относится также шар. Это означает, что у шара ось вращения всегда в отсутствие внешних сил сохраняет фиксированное положение относительно тела и никакой нутации быть не может. Это обусловлено тем, что любая ось, проведенная через центр шара, является центральной главной осью тензора инерции. Нсли тар неоднороден, г. - нуг ии. [20]

Угол нутации Ф при этом следует вводить в формулы осредненным. [21]

Кинетика ХПЯ трет-бу-тилхлорида при стационарном облучении ди-трег-бутилкетона ( а и стационарные нутации при прерывистом фотолизе ( б.| Кинетика изменения сигнала ЯМР ди-грег-бутилкетона при его стационарном фотолизе ( а и стационарные нутации при прерывистом освещении ( б. [22]

Частота нутаций определяется выражением ро [ aij - 0 25 - - 1 / Г) 2 ] / 2, где 0) 14, 7, ц Г2 - времена ядерной релаксации. Если генерация вектора намагниченности происходит не непрерывно, как в предыдущем случае, а в импульсном периодическом режиме с частотой ( в, ро) 1, то при фазочувствительном детектировании наблюдаются стационарные нутации. Такой режим осуществлен в работе [191] при фотолизе ди-г / зег-бутилкетона. На рис. 11.21, а показано изменение сигнала ЯМР грет-бутилхло-рида при непрерывном фотолизе; видно, что сигнал эмиссии, появляющийся в момент включения света, постепенно уменьшается и к моменту выключения света практически исчезает; интенсивность сигналов в этом случае определяется суммарным вкладом эмиссии и поглощения образующихся молекул. В этом случае сигналы нутации соответствуют чистой эмиссии; они исчезают сразу после выключения света. [23]

Частота нутации является резонансной частотой характеристического уравнения. [24]

Частота нутации является показателем качества гироскопа. [25]

К определению вынужденною движения гироскопа. [26]

Угол нутации не зависит от времени и появляется практически мгновенно в момент возникновения внешнего момента Мх. Поэтому угол нутации часто называют нутационным броском. [27]

Явление нутации рассмотрено подробно в цитированных выше книгах Synge, Griffith, Step-hunson. Этот термин также используется для обозначения вибрации двухосевого гироскопа в книге W e e m s, An introduction to the study of gyroscopic instruments. [28]

Будет рассмотрена пассивная нутация вращающегося относительно собственной оси космического корабля, имеющего на борту демпфер колебаний. В более ранней работе [328] Кейн и Барба изучили эффекты, связанные с диссипацией энергии у вращающегося спутника, состоящего из двух упруго соединенных твердых тел. Эта работа относится к одной из основных задач небесной механики - задаче вращения симметричного спутника по круговой орбите. Год спустя, в 1967 г., Роуб и Кейн [329] провели исчерпывающий анализ устойчивости такого упругого спутника. Они показали, что некоторые формы спутников, которые считались устойчивыми при их анализе как твердого тела, с учетом деформируемости оказываются неустойчивыми. [29]

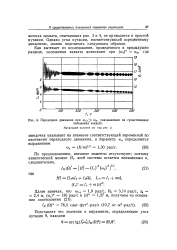Переходное движение при со / ып, указывающее на существование. [30]

Страницы: 1 2 3 4