Область - фазовое пространство
Cтраница 4
Этот вывод аналогичен выводу Гиббса и Больцмана о том, что объем неравновесной области фазового пространства пренебрежимо мал по сравнению с объемом равновесной области ( см. раздел В. [46]
 |
Схематическая иллюстрация временной эволюции точек Пуанкаре из выборки цифровых измерений. [47] |
Мы уже знаем, что если движение хаотично, то траектория стремится заполнить некоторую область фазового пространства. [48]
Наконец, может, например, потребоваться узнать, останется ли система в некоторой области фазового пространства на протяжении всего времени ее работы или нет. [49]
В задачах надежности часто оказывается необходимым вычислять вероятность невыхода изображающей точки системы за пределы некоторой области фазового пространства в течение заданного времени. Указанная вероятность подчиняется уравнению, сопряженному с уравнением ( 63), при заданных краевых условиях на границе области и заданных начальных условиях. [50]
Если затухание в системе недостаточно сильно, точки хаотического аттрактора будут стремиться однородно заполнить некоторую область фазового пространства и структура канторовского множества, характерная для странного аттрактора, не проявится. На рис. 2.11 показан пример такой ситуации при колебаниях изогнутого стержня. Сравнение отображений Пуанкаре, полученных при слабом и сильном затухании, показывает, что иногда усиление затухания может вызвать появление фрактальной структуры. [51]
Ранее мы познакомились с ситуацией, в которой сколь угодно малое возмущение приводит к образованию областей фазового пространства, внутри которых динамика системы является стохастической. [52]
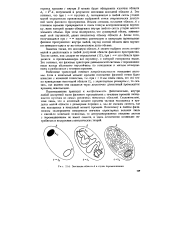 |
Эволюция области А в случае перемешивания. [53] |
Заметим также, что исходную область А можно выбрать сколь угодно малой и расположить в любой доступной области фазового пространства. Тем не менее, как следует из определения ( 15), при t - эта область превратится в пронизывающую все паутинку, о которой говорилось выше. Это означает, что фазовые трактории динамической системы с перемешиванием всегда абсолютно неустойчивы по отношению к малым возмущениям и разбегаются с течением времени. [54]
Генерирование модели / ( to, Cj), претендующей аппроксимировать процесс в / - и области фазового пространства. Здесь т - порядковый номер модели-претендента, определяющий к тому же ее сложность. [55]
Вероятности переходов между состояниями случайного процесса определяются кинетическими скоростями химических реакций, а законы сохранения задают область фазового пространства, где происходят изменения данного случайного процесса. [56]
При таком распределении плотность вероятности отлична от нуля и равна 1 / Q - ДЕ внутри области фазового пространства объема ДГ Q ДЕ и равна нулю вне этой области. [57]
Страницы: 1 2 3 4