Математическая обработка - экспериментальные данные
Cтраница 3
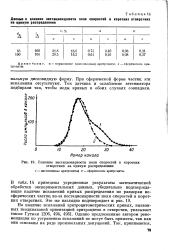 |
Влияние нестационарности поля скоростей в коротких отверстиях на кривую распределения. [31] |
В табл. 14 приведены усредненные результаты математической обработки экспериментальных данных, убедительно подтверждающие наличие искажений кривых распределения по размерам несферических частиц из-за нестационарное поля скоростей в коротких отверстиях. [32]
Математическая статистика, и, в частности, математическая обработка экспериментальных данных как ее составная часть, базируются на многих разделах математики и прежде всего на теории вероятностей. Предполагается, что читатель знаком с такими основными понятиями теории вероятностей, как случайные события и величины, вероятность события, операции над случайными событиями, случайными величинами и вероятностями, законы распределения случайных величин, предельные теоремы теории вероятностей. Некоторые дополнительные сведения из теории вероятностей, используемые в математической статистике, будут вводиться в соответствующих местах монографии по мере необходимости. [33]
В зависимости от цели и требуемой точности для математической обработки экспериментальных данных можно использовать графические или статистические методы. [34]
В таблице приведены значения коэффициентов теплопередачи, полученные путем математической обработки экспериментальных данных. [35]
Столь длительный период накопления знаний объясняется прежде всего различным уровнем возможности математической обработки экспериментальных данных в физике и химии. Кроме того, мир веществ очень многообразен, и в центре научных интересов химиков находилось исследование свойств, строения и превращений веществ. В течение десятилетий закон простых кратных отношений удовлетворительно объяснял превращения веществ. Поэтому Бертолле, пытавшийся найти зависимость между массой и химическими свойствами веществ, оставался непонятым современными ему химиками. [36]
Было сделано много попыток подойти к установлению общих закономерностей процессов элиминации путем математической обработки экспериментальных данных по выделению ядов из организма. В общем процесс элиминации подчиняется экспоненциальному закону, выражаясь кривой, стремящейся к нулю. В то же время скорость выделения различна для разных ядов, в том числе и металлов. Экспоненциальный закон выделения представляется уравнением: С C0 - e - Kt, где С - концентрация вещества через t минут, С0 - начальная концентрация вещества в крови, К - - константа скорости выделения, е - основание натуральных логарифмов. [37]
Было сделано много попыток подойти к установлению общих закономерностей процессов элиминации путем математической обработки экспериментальных данных по выделению ядов из организма. В общем процесс элиминации подчиняется экспоненциальному закону, выражаясь кривой, стремящейся к нулю. В то же время скорость выделения различна для разных ядов, в том числе и металлов. Экспоненциальный закон выделения представляется уравнением: С С0 e - Kt, где С - концентрация вещества через t минут, С0 - начальная концентрация вещества в крови, / С - константа скорости выделения, е - основание натуральных логарифмов. [38]
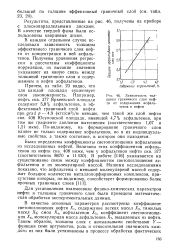 |
Зависимость толщины граничного слоя нефти от содержания асфальтенов в нефти. [39] |
Для установления взаимосвязи физико-химических параметров лефти и толщины граничного слоя была проведена математическая обработка экспериментальных данных. [40]
Часть уравнений основывается на теоретических представлениях, но большинство найдено в результате математической обработки экспериментальных данных. [41]
В предлагаемых лабораторных работах общий вид функции обычно известен и поэтому задача математической обработки экспериментальных данных сводится к определению параметров этой функции, полученных на основании экспериментальных данных. [42]
 |
Зависимость вязкости г водноспиртового раствора от концентрации q в нем этилового спирта. [43] |
К настоящему времени в литературе накоплена значительная информация о способах обобщения и математической обработки экспериментальных данных по вязкости неньютоновских систем. Рассмотрим наиболее приемлемые из них для инженерной практики. Из закона Ньютона следует, что для определения вязкости опытным путем необходимо знать величину приложенного касательного напряжения и значение имевшего при этом место градиента скорости. [44]
Часть уравнений основывается на теоретических представлениях, но большинство было найдено в результате математической обработки экспериментальных данных. [45]
Страницы: 1 2 3 4