Октада

Cтраница 1

Октады, построенные по 24, образуют систему Штейнера 5 ( 5, 8, 24) ( разд. Очень важно научиться определять октаду по ее 5 заданным точкам. Эта задача легко сводится к 3-задачам и 5-задачам, если заметить, что изменение счета в данном столбце достигается заменой по крайней мере одной точки в столбце и по крайней мере двух точек, если к тому же требуется сохранить четность столбца. [1]

Октада и дополнительный к ней квадрат связаны тем фактом, что имеется взаимно однозначное соответствие между разбиениями октады на две тетрады и квадрата на четыре параллельные двумерные плоскости, заданными требованием, чтобы образующееся семейство из шести тетрад было секстетом. На рис. 11.17 мы приводим все эти 35 секстетов. Это позволяет легко дополнить до тетрады любые три ее точки. [2]

Одна октада О, 1, 2, 3, 4, 7, 10, 12 уже найдена, и поэтому по теореме 5 каждое 5-элементное множество содержится по крайней мере в одной октаде. [3]

Далее, поскольку две октады пересекаются по 0, 2, 4 или 8 точкам, любая октада есть либо объединение двух тетрад из S, либо содержит по две точки каждой из четырех тетрад или же три из одной тетрады и по одной из каждой из остальных. [4]

Группа 24А8, оставляющая на месте октаду, является 6 1 -, 3 2 - и 1 -транзитивной на октаде и на ее дополнении. [5]

Последнее утверждение теоремы 9 гласит, что октады образуют систему Штейнера 5 ( 5 8 24) ( разд. [6]

В случае ( i) S есть специальная октада Sa - Группа М24 тран-зитивна на таких множествах. [7]

Рис, 11.36. Как гексада превращается в октаду. [8]

Мы просто пользуемся тем фактом, что если октада содержит четыре из неподвижных точек и две точки, подвергшиеся транспозиции, то оставшиеся две точки тоже должны быть затронуты транспозицией этой перестановки. [9]

На рис. 11.16 изображены ( а) наша стандартная октада и ( Ь) ее дополнение - стандартный квадрат - и стандартное начало в этом квадрате. [10]

В случае ( ii) S получается из специальной октады S Т добавлением одной точки и удалением другой. [11]

По-видимому, стоит поподробнее остановиться на способе, которым октада восстанавливается по слову гексакода в рассматриваемом примере. [12]

В случае ( iii) S Г; - специальная октада, если Т содержит две точки из S и две из его дополнения, и умбральная додекада, если Г, не пересекается с S. Подсчет точек из S показывает, что имеется четыре тетрады первого типа и две - второго, так что S может быть получено ( двумя способами) удалением четырех точек из умбральной додекады. [13]

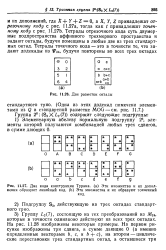Две разметки октады. [14]

Тетрады отрезочного кода суть двумерные подпространства аффинного трехмерного пространства и задают октады, будучи помещены в любые две из трех стандартных октад. [15]

Страницы: 1 2 3 4