Бистабильность

Cтраница 1

Бистабильность наблюдается и в гидродинамической модели диода Пирса при п - 1 0 и наличии внешней запаздывающей обратной связи. Такая система подробно была исследована в работах [145, 146] ( см. также лекцию 4 первого тома) и в ней была обнаружена в определенном диапазоне управляющих параметров неоднозначность наблюдающегося режима. [1]

Неустойчивость и бистабильность определяются как свойства макроскопического уравнения. Влияние флуктуации сводится просто к тому, что они заставляют систему сделать выбор между той или иной макроскопически устойчивой точкой. [2]

Следовательно, данная бистабильность соответствует той, которая существует и при детерминированных внешних условиях. [3]

Покажите, что бистабильность может существовать и в этом случае. [4]

Примерами реализации схемкой бистабильности с оптической обратной связью могут служить схемы с ПВМС, разработанные С. [5]

Чтобы существовала область бистабильности, функция Y ( X) должна быть немонотонной. [6]

Были обнаружены явления динамической бистабильности и тристабильности - скачкообразных переходов с одного стационарного режима протекания реакции на другой, релаксационные колебания, бегущие волны, хаотические колебания и др. Впрочем анализ этих явлений выходит за рамки краткого представления о кинетике автоколебательных реакций и компетентности автора. [7]

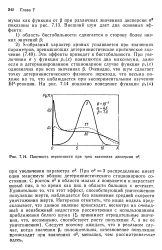Плотность вероятности при трех значениях дисперсии а2. [8]

Эти эффекты приводят к бистабильности. Очевидно, чтю шум сдвигает точку детерминистического фазового перехода, что весьма похоже на то, что наблюдается при экспериментальном изучении БР-реакции. [9]

На этом основано свойство бистабильности - один и тот же резонатор может и аккумулировать энергию излучения, и пропускать ее при разных мощностях поля. [10]

Мы не рассматриваем другой возможности бистабильности и гистерезиса - изменение отстройки вблизи порога генерации. Хотя этот случай более сложный, его качественные особенности можно исследовать методом, аналогичным изложенному здесь. [11]

Отношение между входной и выходной амплитудами [ ]. R Каждая кривая соответствует определенному значению aL 2СТ.| Сравнение экспериментальных и теоретических результатов для двух значений интенсивности У. ( квадраты и Y, ( ромбы в точках переключения как функций параметра кооперативности С ( Orozco, Kimble and Rosenberger, 1987. [12]

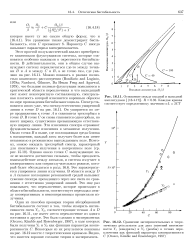
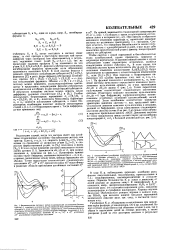
Один из способов проверки теории абсорбционной бистабильности состоит в том, чтобы измерить интенсивности света YI, У, соответствующие точкам А и D на рис. 16.11, где имеет место переключение из одного состояния в другое. Это было сделано в экспериментах ( Orozco, Kimble and Rosenberger, 1987), в ходе которых были получены У и Y2 как функции параметра кооперативности С. Некоторые из их результатов показаны на рис. 16.12 вместе с теоретическими кривыми. Видно, что имеется хорошее согласие теории и эксперимента. [13]

Ферментативная система с тремя стационарными состояниями ( биохим. триггер а зависимое 1Ь скорости Л / А изменения безразмерной концентрации субстрата И. от ее значения ( о при разл скоростях ( а поступления субстрата, пунктиром обозначены кривые, соответствующие бифуркац значениям а и а [, б-зависимость стационарных значений о. от с. а. 1 и а. 3 устойчивые, о 2 неустойчивое стационарные состояния. [14]

Чтобы система с одной переменной и бистабильностью стала колебательной, нужно превратить параметр в медленную переменную. Точки пересечения нуль-изоклин соответствуют стационарным состояниям системы. Этим колебаниям соответствует замкнутая траектория движения системы-т. Сплошными линиями показаны нуль-изоклины в ситуации, далекой от бифуркации, когда единственное стационарное состояние системы ( точка О на рис. 2, а) сильно неустойчиво и окружено предельным циклом АВСО. [15]

Страницы: 1 2 3 4 5