Определитель - гурвиец
Cтраница 2
Последнее неравенство, являясь развернутым определителем Гурвица, представляет собой необходимое и достаточное условие сходимости процессов и устойчивости систем. Если это неравенство не выполняется, процессы становятся расходящимися, а система регулирования неустойчивой. [16]
Определителем этой системы будет определитель Гурвица, составленный из коэффициентов характеристического полинома М ( р) с чередующимися знаками. [17]
Все эти определители называются определителями Гурвица. Заметим, что последний определитель Д включает в себя всю матрицу целиком. [18]
И наоборот, если все определители Гурвица равны нулю, то все коэффициенты полинома (5.5) с нечетными индексами равны нулю. [19]
Дп-2 представляют собой диагональные миноры определителя Гурвица. [20]
Кроме того, необходимо, чтобы определитель Гурвица второго порядка был также больше нуля. [21]
Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров. [22]
Коэффициент аг входит в положительный член предпоследнего определителя Гурвица, а0 - в отрицательный, причем а1 суммируется еще с рядом параметров, а а0 - нет. Гурвица и, следовательно, сужает область значений i, при которых сохраняется устойчивость равновесия привода. Уменьшение i в соответствии с формулой ( II 1.52) увеличивает зону нечувствительности и ошибку слежения в установившихся режимах. Кроме того, увеличение массы подвижных частей, как известно, ухудшает динамические характеристики привода, увеличивая динамическую ошибку и время переходного процесса. Поэтому для повышения точности гидравлических следящих приводов желательно конструктивными мерами и выбором соответствующих материалов по возможности уменьшать массу подвижных частей. [23]
Определитель Л, который принято называть определителем Гурвица, составляется по следующему правилу. На главной его диагонали выписываются коэффициенты уравнения в том порядке, в котором они расположены в уравнении, начиная с коэффициента a i - i - В каждом из столбцов определителя под диагональным элементом выписываются коэффициенты с возрастающими, а над ними - с убывающими индексами. Все коэффициенты, индексы которых превышают п или индексы которых отрицательны, заменяются нулями. [24]
Так как выполняется необходимое условие устойчивости и единственный определитель Гурвица с четным индексом положителен, то по критерию Льенара-Шипара линеаризованная система устойчива. Следовательно, и исходная нелинейная система асимптотически устойчива. [25]
 |
Анализ устойчивости по годографу Найквиста ( а и по логарифмическим частотным характеристикам ( б. [26] |
При равенстве нулю хотя бы одного из определителей Гурвица система находится на границе устойчивости. [27]
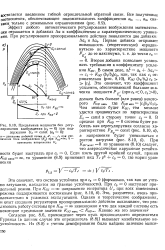 |
Предельные мощности без регулирования возбуждения ( ct 0 при поддержании. / г const ( с3 0. [28] |
Согласно рис. 8.6, прохождение через нуль предпоследнего определителя Гурвица [ в данном случае это определитель (8.8) ] вызывает колебательную неустойчивость. [29]
Нетрудно видеть, что определитель Д равен определителю Дп Гурвица. [30]
Страницы: 1 2 3 4