Определитель - гурвиец
Cтраница 3
Последовательные главные миноры матрицы Я обычно называются определителями Гурвица. [31]
В этом случае коэффициенты характеристического уравнения и второй определитель Гурвица тождественно больше нуля и все исследование сводится к анализу третьего определителя. [32]
Математическое условие устойчивости периодического решения предполагает положительность всех определителей Гурвица, кроме предпоследнего, который должен быть положительным при величине амплитуды большей расчетной и отрицательным - при амплитуде меньшей расчетной. Невыполнение этого условия свидетельствует о неустойчивости найденного периодического решения. [33]
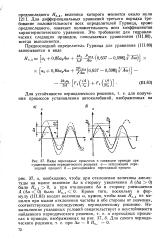 |
Виды переходных процессов в следящем приводе при существовании периодического решения. а-затухающий переходный процесс. б - расходящийся переходный процесс. [34] |
Для дифференциальных уравнений третьего порядка требование положительности всех определителей Гурвица, кроме предпоследнего, означает положительность всех коэффициентов характеристического уравнения. Это требование для гидравлических следящих приводов, описываемых уравнением (III.80), всегда выполняется. [35]
В справедливости этого утверждения можно убедиться, последовательно вычисляя определители Гурвица, начиная с определителя 1-го порядка. [36]
Уменьшение коэффициента падения силы трения с возрастанием скорости увеличивает предпоследний определитель Гурвица, поэтому это всегда выгодно с точки зрения устойчивости. С другой стороны, величина мало сказывается на установившейся ошибке привода по скорости. В связи с этим желательно по возможности уменьшать коэффициент падения силы трения от скорости. [37]
Параметры системы изменяются в таких областях, для которых предпоследний определитель Гурвица & п г для характеристического уравнения гармонически линеаризованной системы может равняться нулю или иметь любой знак. Для систем третьего или четвертого порядка это равносильно условию положительности всех коэффициентов уравнений. [38]
Варьируем коэффициенты f ( z) так, чтобы все определители Гурвица стали отличными от нуля и чтобы те из них, которые до варьирования были отличны от нуля, сохранили свои знаки при варьировании. [39]
 |
Кривая Михайлова. [40] |
Достоинства критерия Михайлова проявляются при исследовании систем высокого порядка, когда определители Гурвица требуют большого объема вычислений. [41]
Уравнение для определения амплитуды автоколебаний может быть получено из условия равенства предпоследнего определителя Гурвица нулю, что соответствует границе колебательной неустойчивости. [42]
Дь - определители, образуемые отчеркиванием k строк и столбцов в определителе Гурвица. [43]
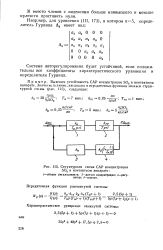 |
Структурная схема САР концентрации SO2 в контактном аппарате. [44] |
Система авторегулирования будет устойчивой, если положительны все коэффициенты характеристического уравнения и определители Гурвица. [45]
Страницы: 1 2 3 4