Неадиабатический переход

Cтраница 1

Неадиабатические переходы могут, разумеется, происходить и при колебательных энергиях Е, меньших порогового значения Ео. В этом случае они представляют часть процесса активации молекулы. [1]

Неадиабатическим переходам, очевидно, благоприятствуют малые энергии резонанса, большие скорости и большие отличия в наклонах пересекающихся кривых потенциальной энергии. [2]

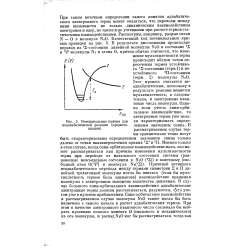Потенциальные кривые для неадиабатической реакции ( предиссо-циация. [3]

Причиной истинного неадиабатического перехода между термами симметрии S и П линейной трехатомной молекулы могло бы явиться ( если бы мультиплетность термов была одинакова) взаимодействие вращения молекулы с электронным моментом количества движения. В случае большого спин-орбитального взаимодействия адиабатические электронные термы должны рассчитываться, разумеется, с его учетом уже в нулевом приближении. [4]

Для этого случая неадиабатические переходы локализованы в области квазипересечения термов, так что для расчета вероятности можно воспользоваться результатом задачи 2.23. При этом необходимо учесть, во-первых, что область квазипересечения проходится атомами дважды - при их сближении и разлете и, во-вторых, что скорость vp в точке квазипересечения следует выражать через скорость атомов на бесконечности и прицельный параметр. [5]

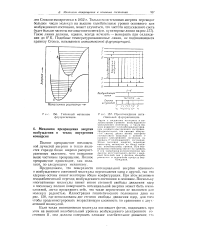Происхождение антистоксовой флуоресценции. [6]

При этом возможен неадиабатический переход возбужденного состояния в основное. Поскольку многоатомные молекулы имеют много степеней свободы движения ядер и поскольку полная поверхность потенциальной энергии может быть очень сложной, легко представить себе, что такие пересечения не являются для молекул редкостью. Иллюстрация гипотетического положения дана на рис. 158, где использованы две степени свободы движения ядер, для того чтобы продемонстрировать возрастающую сложность по сравнению с двухатомной молекулой. [7]

Поскольку квантовомеханические приближения неадиабатических переходов довольно сложны, некоторые авторы сформулировали феноменологические модели, основанные главным образом на статистической теории атома. Дело в том, что при квазиунругих столкновениях небольшая часть кинетической энергии относительного движения превращается во внутреннюю ( электронную) энергию. Оценки этой энергии в рамках статистических моделей [22- 24] оказываются более полезными, чем проведенные до сих пор квантовомеханические вычисления. В этих моделях постулируется, что в процессе возбуждения при столкновении участвует несколько электронов и что в результате безызлучательных переходов система оказывается в возбужденном или ионизованном состоянии после того, как компоненты расходятся. [8]

Поскольку квантовомеханические приближения неадиабатических переходов довольно сложны, некоторые авторы сформулировали феноменологические модели, основанные главным образом на статистической теории атома. Дело в том, что при квазиупругих столкновениях небольшая часть кинетической энергии относительного движения превращается во внутреннюю ( электронную) энергию. Оценки этой энергии в рамках статистических моделей [22- 24] оказываются более полезными, чем проведенные до сих пор квантовомеханические вычисления. В этих моделях постулируется, что в процессе возбуждения при столкновении участвует несколько электронов и что в результате безызлучательных переходов система оказывается в возбужденном или ионизованном состоянии после того, как компоненты расходятся. [9]

Если же скорость неадиабатических переходов меньше скорости колебательного возбуждения, то вполне возможно, что именно она будет определять скорость реакции. [10]

При этом скорость неадиабатического перехода между основным и этими возбужденными состояниями должна быть больше скорости диссоциации. [11]

Аналогичный механизм, включающий неадиабатический переход между отталкивателышм и возбужденным стабильным электронным состояниями, был рассмотрен в [343] для радиационной рекомбинации атомов О и Н при очень низких температурах. При этом вследствие сравнительно малой массы Н неадиабатический переход происходит туннельным образом. [12]

Эту нечеткость в определении неадиабатических переходов и реакций, установившуюся в литературе, необходимо всегда иметь в виду ( см. примечание на стр. В дальнейшем мы ограничимся случаями малого спин-орбитального взаимодействия и будем понимать под адиабатическими термами такие электронные состояния, которые характеризуются определенным значением полного электронного спина. В этих случаях спин-орбитальное взаимодействие, так же как и динамическое взаимодействие электронов и ядер, должно рассматриваться как причина неадиабатических переходов. [13]

Заметим, что для неадиабатических переходов, индуцируемых динамическим взаимодействием ядер и электронов, матричный элемент должен зависеть от скорости ядер и возрастать вместе с ней. [14]

Процессы такого типа называются неадиабатическими переходами, поскольку они являются следствием условий, несовместимых с принципом адиабатичности. Мы увидим в дальнейшем, что такие переходы осуществляются довольно часто. Так, например, они должны осуществляться, когда свет превращается в тепло, не индуцируя фотохимических реакций или не вызывая флуоресценции. Фосфоресценция органических соединений включает, по-видимому, неадиабатический переход из возбужденного синглетного состояния в триплетное с последующим испусканием света ( см. стр. Всегда, когда поверхности потенциальной энергии различных электронных состояний молекулы пересекаются, следует учитывать возможность неадиабатического перехода. [15]

Страницы: 1 2 3 4