Неадиабатический переход

Cтраница 2

Возмущение колебательных уровней вследствие пересечения кривых потенциальной энергии.| Вид колебательно-вращательных полос в спектре, обусловленном переходами из некоторого состояния х на разные колебательные уровни состояния АОВ на 116. [16]

Это размазывание уровней энергии вследствие неадиабатических переходов между континуумом и устойчивым состоянием называется предиссо-циацией. [17]

Адиабатическое ( г и неадиабатическое ( о движение п области наибольшего сближения двух потенциальных кривых. [18]

Наоборот, при быстром движении ядер вероятность неадиабатических переходов значительно повышается. [19]

Как видно из этой формулы, вероятность неадиабатического перехода очень быстро уменьшается с увеличением наименьшего расстояния 2а между потенциальными кривыми и с уменьшением относительной скорости v движения ядер. [20]

Проведено обсуждение простого критерия неадиабатичности и моделей неадиабатических переходов. Выделены существующие трудности в количественной оценке наблюдаемых довольно больших значений поперечных сечений процессов ионизации и возбуждения. [21]

Основное усовершенствование, введенное в настоящей теории неадиабатического перехода электрона, относится к вопросу о перегруппировке растворителя. [22]

Пересечение адиабатических термов. [23]

Подстановка выражения (10.5) в (10.4) позволяет выразить вероятность неадиабатического перехода через прицельный параметр, вычислить сечение и затем константу скорости неадиабатического процесса. При этом нужно учесть, что при атомных столкновениях точка пересечения проходится дважды: первый раз при сближении атомов, второй раз - при разлете. Поэтому при вычислении сечения в качестве вероятности перехода должна быть использована величина Ij2 означающая вероятность двойного прохождения системой области4 пересечения термов. [24]

Для больших 12 задача не решена, однако вероятность неадиабатического перехода при этом очень мала и не играет роли в химической кинетике. [25]

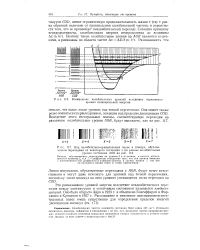
На рис. 5.8, в изображен еще один случай неадиабатических переходов. [26]

Однако для столкновения молекул с химически активными атомами области неадиабатических переходов могут быть локализованы на сравнительно небольших расстояниях. Ясно, что существование областей сильной неадиабатической связи, лежащих до достижения системой потенциального барьера, перевал через который ведет к реакции, должно корректным образом учитываться при описании динамики реакции. [27]

Вблизи пересечения параметр Месси оказывается малым, что позволяет неадиабатическим переходам проходить с большой эффективностью. [28]

В тех областях, где условие 5 1 нарушается, неадиабатические переходы могут происходить с большой вероятностью. [29]

Как и следовало ожидать, при больших скоростях движения вероятность неадиабатического перехода близка к единице. [30]

Страницы: 1 2 3 4