Периодограмма

Cтраница 1

Периодограмма широко используется для построения различного рода оценок для / ( Я), / ( Я) и критериев для проверки гипотез об этих характеристиках. [1]

Периодограмма является асимптотически несмещенной оценкой спектральной плотности и при неизвестном т, однако эти оценки не являются состоятельными. [2]

Периодограммы всех сегментов усредняются. [3]

Периодограмма должна дать острый пик на частоте / - / Т цикла в единицу времени. [4]

Периодограмма S, ( со) является асимптотически несмещенной, но несостоятельной оценкой спектральной плотности. [5]

Сглаженной периодограмме Gx ( j) соответствует рассмотренная нами оценка 5G ( /), которая существенно не отличается OTt Gx ( f) по своим свойствам. [6]

Каждая периодограмма характеризует количество гармонических составляющих определенной длины волны и амплитуды в спектре соответствующей деформации. Изменение параметров периодограмм указывает на проявление материалом существенно нелинейных свойств, отражает кинетику диссипатив-ных структур в виде таких явлений, как синхронизация, стохастичность, самоорганизация, указывает на количественную связь диссипативных структур и механических свойств материала. [7]

Сглаживание периодограммы 2Gx ( f) по частотному интервалу представляет собой операцию свертывания ее с некоторой весовой функцией, которая определяет вид сглаживания и соответствующую сглаженную оценку. [8]

Детальный график периодограммы t ( to) ряда Бевериджа, рассматриваемой уже как функция частоты, может быть найден, в частности, в [ 101, рис. 49.1 ] и [ 9, рис. А. В тех же двух книгах, а также в книгах [78, 256] и в целом ряде других книг и журнальных статей ( см., в частности, примечание 116 можно найти целый ряд дополнительных примеров периодограмм IT ( со) стационарных временных рядов х ( t); все они оказываются крайне нерегулярными функциями частоты. [9]

Изменение параметров периодограмм ( амплитуда, частота, фаза) указывает на проявление обрабатываемой сталью существенно нелинейных диссипативных свойств, определяет связь диссипативных структур и механических свойств, позволяет количественно характеризовать диссипативные структуры в стали. Методически в данной работе понятие конструкционной прочности предполагает ряд количественных характеристик, описывающих работу стали в конструкции и определяемых как устойчивость и самоорганизация днссипативных структур при различных условиях нагружения. [10]

Таким образом, периодограмма не является хорошей оценкой 8уу ( е а), так как ее стандартное отклонение является величиной того же порядка, что и величина, подлежащая оценке. Аналогично можно показать, что оценка Syy также несостоятельна. [11]

Сама идея сглаживания периодограммы при помощи весовой функции с целью получения состоятельных оценок спектральной плотности мощности основана на выборе некоторого частотного интервала Af, в котором можно разместить много независимых спектральных составляющих, и на вычислении среднего этих составляющих. [12]

Третья возможность использования периодограммы заключается в том, чтобы усреднить значения периодограммы, вычисленные с шагом Af - - l / 7 по частотному интервалу. Если в интервале усреднения Д / э укладывается k независимых значений периодограммы, то при условии, что смещение оценки мало, мы получим статистическую точность примерно такую же, как при усреднении по множеству, но разрешающая способность анализа будет уже определяться величиной порядка 1 / тт. [13]

Удобным методом сглаживания периодограммы является применение треугольной весовой функции. [14]

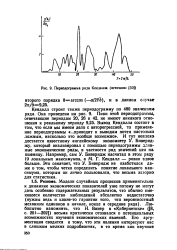Периодограмма ряда Кендалла ( источник. ( 50 ]. [15]

Страницы: 1 2 3 4