Периодограмма

Cтраница 2

Кендалл строит также периодограмму по 480 значения ряда. И тут неплохо достается известному английскому экономисту У. [16]

В случае рядов, периодограммы которых изображены на рис. 19 а и 19 б, мы, разумеется, не знаем истинной формы спектральной плотности и можем лишь догадываться, что она должна быть гораздо более гладкой, чем соответствующая периодограмма. [17]

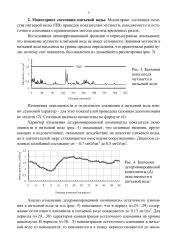Значения показателя мутности в питьевой воде.| Значения детерминированной компоненты ( dt окисляемости в питьевой воде. [18]

Исследование автокорреляционной функции и периодограммы показывают, что изменение мутности в питьевой воде не имеет сезонности. [19]

Для взвешенных сегментов вычисляются модифицированные периодограммы. [20]

Исследование основано на анализе периодограмм микропластических деформаций в стали после различных термических обработок. [21]

Отсюда становится понятным, что периодограмма не может служить удовлетворительной оценкой спектральной плотности. [22]

Мы видим, что обе периодограммы iT ( со) имеют крайне нерегулярную форму, причем их колебания относительно гладкой кривой / ( со) не имеют ничего общего друг с другом. Все эти рисунки наглядно показывают, насколько плохой оценкой спектральной плотности является периодограмма; при этом, в силу сказанного выше ( см., в частности, равенство (2.266) и примечание 114), с ростом длины Т используемой реализации поведение периодограммы iT ( со) должно становиться все более и более нерегулярным. [23]

Отсюда становится понятным, что периодограмма не может служить удовлетворительной оценкой спектральной плотности. [24]

В [10] показано, что периодограмма не является состоятельной оценкой спектральной плотности мощности, поскольку дисперсия такой оценки сравнима с квадратом ее математического ожидания. С ростом числа используемых отсчетов значения периодограммы начинают все быстрее флуктуировать. [25]

Отсюда становится понятным, что периодограмма не может служить удовлетворительной оценкой спектральной плотности. [26]

Авторегрессионная модель формирования сигнала. [27]

Так же как и для периодограммы Бартлетта, дисперсия оценки, получаемой методом Уэлча, уменьшается примерно пропорционально числу сегментов. Благодаря перекрытию в методе Уэлча используется больше сегментов, поэтому дисперсия оценки спектра плотности мощности оказывается меньше, чем для метода Бартлетта. [28]

Таким образом, для построения периодограмм, по Шустеру, желательно теоретическое знание выявляемых в ряду наблюдений гармоник, для чего предварительно следует либо установить связь с факторами, характеризующимися циклическими колебаниями, либо провести автокорреляционный или спектральный анализ рядов и вскрыть имеющуюся в них цикличность. [29]

График зависимости gk от k называют нормированной кумулятивной периодограммой. [30]

Страницы: 1 2 3 4