Эллиптическая пластинка
Cтраница 3
Так, в работе [31] - приведены результаты изучения собственных поперечных колебаний тонких ортотроп-ных эллиптических пластинок с аналогичным эквидистантным вырезом. Теоретический анализ осуществлен с использованием метода Ритца. При этом проведено преобразование эллиптической пластинки в кольцевую с единичным внешним радиусом путем перехода к новой системе координат. Кольцевая круговая пластинка разбита на ряд секторов. Поперечные перемещения аппроксимируются рядами произведений приемлемых функций секториальнрй балки с малым углом конусности в плане на тригонометрические функции угловой координаты. Перемещения в направлении радиальной координаты аппроксимируются полиномами пятой степени, которые удовлетворяют основному уравнению изгибных колебаний балок. В результате проведенного исследования определены собственные числа и формы собственных колебаний для некоторых образцов изотропных эллиптических и круговых пластинок с подобными центральными вырезами. Для апробации полученных авторами результатов в работе дано сопоставление с результатами точных решений и результатами других авторов, полученных для частных случаев. [31]
Настоящая работа является дальнейшим развитием недавно разработанного метода, ранее изложенного в публикациях [1, 2] для исследования изгиба и устойчивости тонких упругих пластинок. Предлагаемый метод представляется мощным аппаратом для исследования таких динамических задач, сложная математическая трактовка которых не позволяет решать их аналитическими или другими численными методами. Применение метода продемонстрировано для случая эллиптической пластинки как с защемленными, таК и с-шарнйрно опертыми краями. [32]
В работе [26] изложен упрощенный приближенный метод решения задач о колебаниях двусвязных пластинок произвольной формы. В дальнейшем этот метод использован автором [27] для изучения поведения двусвязных пластинок различной геометрии. Вычисления были выполнены для нескольких примеров: кольцеобразной эллиптической пластинки, круговой пластинки с эллиптическим вырезом, квадратной пластинки с эллиптическим вырезом. [33]
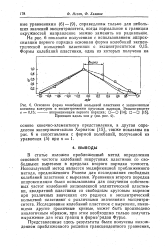 |
Основная форма колебаний кольцевой пластинки с защемленным внешним контуром и эксцентрическим круговым вырезом. Эксцентриситет. [34] |
В статье изложен приближенный метод определения основной частоты колебаний некругрвых пластинок со свободными вырезами в пределах второго порядка точности. Используемый метод является модификацией приближенного метода, предложенного Рэлеем для исследования свободных колебаний пластинок с вырезами. Уравнения второго порядка аппроксимации были использованы для получения собственных частот колебаний защемленной эллиптической пластинки, квадратной пластинки со свободным круговым вырезом при различных значениях его радиуса и эксцентрической кольцевой пластинки с различными значениями эксцентриситета. Исследование колебаний пластинок с вырезами, имеющими другие граничные кривые, может быть произведено аналогичным образом, при этом необходимо только получить выражение для этих границ в форме рядов Фурье. [35]
 |
Псилот голый ( Psilotum nudum. Веточка с сппангиями ( увел..| Тмезиптерис ( Tmesipteris tannensis. [36] |
С эволюционной точки зрения большой интерес представляет вопрос о листовых органах псилотовых. На стеблях псилота, главным образом в верхней части, видны мелкие чешуевидные придатки, расположенные без определенного порядка. Они лишены как устьиц, так и жилок. В нижней части стебля они мелкие и чешуевидные, как у пси-лота, но выше становятся крупнее и представляют собой уплощенные латерально ( в вертикальной плоскости) и нисходящие на стебель ланцетные или эллиптические пластинки, кончающиеся остроконечием. За исключением нижних чешуевидных придатков, они имеют хорошо выраженную жилку, представляющую собой одиночный проводящий пучок. [37]
В статье разработан приближенный метод определения основных частот собственных колебаний пластинок со свободными круговыми вырезами. Внешняя граница пластинок предполагается незначительно отличающейся от круговой. Приближенные выражения для радиусов каждой ограничивающей кривой выражены через ряды Фурье. Граничные условия, записанные модифицированными рядами для формы кругового кольца, удовлетворяются приближенным образом на внутреннем и внешнем краях пластинки. Приближенное характеристическое уравнение ( либо первого, либо второго порядка аппроксимации) получается в результате удовлетворения граничным условиям, а основная частота колебаний определяется как первый корень соответствующего характеристического уравнения. Для демонстрации решения, основанного на аппроксимации второго порядка, определены приближенные частоты основной формы колебаний защемленной эллиптической пластинки, квадратной пластинки с круговым вырезом и, круговой пластинки с эксцентрическим круговым вырезом. Для последней также получено решение, основанное на аппроксимации первого порядка для основной формы колебаний. [38]
Страницы: 1 2 3