Плотность - распределение - случайная величина
Cтраница 1
Плотность распределения случайной величины р ( х) равна нулю вне отрезка [1,3; 2,7] и р ( дг) Л на этом отрезке. [1]
Плотность распределения случайной величины р ( х) равна нулю вне отрезка [1,3; 2,7] и p ( x) h на этом отрезке. [2]
Плотность распределения случайной величины полностью определяет случайную величину. [3]
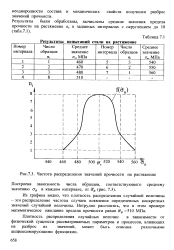 |
Результаты испытаний стали на растяжение. [4] |
Плотность распределения случайных величин в зависимости от физической сущности рассматриваемых параметров и процессов, влияющих на разброс их значений, может быть описана различными аппроксимирующими функциями. [5]
Плотность распределения случайной величины полностью определяет случайную величину. [6]
Обозначим плотность распределения случайной величины Qzf ( qz; v, 8Z), где v / i - / - число ст. св. [7]
Найти плотности распределения случайных величин X и F, а также их условные плотности распределения относительно друг друга. [8]
Если известна плотность распределения случайной величины или заданы вероятности значений дискретной величины, то может оказаться, что математическое ожидание удобнее вычислять не по сформулированным выше определениям, а по формулам, которые мы получим в качестве частных случаев следующих двух теорем. [9]
Функции, описывающие плотности распределения случайных величин, имеющих распределения хи-квадрат, Стьюдента и Фишера, сложны. [10]
Как находится плотность распределения случайной величины Y, если эта случайная величина есть монотонная функция случайной величины X, закон распределения которой известен. [11]
 |
Графики нагрузок приемников электроэнергии. [12] |
Параметры закона плотности распределения случайных величин оценивают экспериментальным путем. [13]
Если уже известна плотность распределения случайной величины или вероятности значений дискретной величины, то может оказаться, что математическое ожидание удобнее вычислять не по определению, а по формулам, которые мы получим в качестве частного случая следующих двух теорем. [14]
Эта функция называется плотностью распределения случайной величины. В ее определении участвует предел, который не всегда существует. [15]
Страницы: 1 2 3 4