Плотность - распределение - случайная величина
Cтраница 3
Формула (4.51) позволяет сделать вывод о том, что плотность распределения случайной величины однозначно определяется ее характеристической функцией. [31]
Формула (20.19) может быть применена в тех случаях, когда плотность распределения случайной величины транспортной партии ( которая соответствует частоте попадания / j случайных значений грузопотока в интер. [33]
Пользуясь критериями согласия, проверяют степень согласованности статистической и теоретической плотностей распределения случайных величин, определяют законы распределения и их параметры. [34]
При каком значении а функция f ( x) является плотностью распределения случайной величины X. Определить начальные и центральные моменты первых четырех порядков, асимметрию и эксцесс. [35]
При каком значении а функция f ( x) является плотностью распределения случайной величины X. Определить начальные и центральные моменты первых четырех порядко. [36]
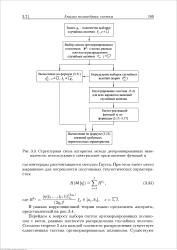 |
Структурная схема алгоритма метода детерминированных эквивалентов, использующего спектральное представление функций г ]. [37] |
Перейдем к вопросу выбора систем ортонормированных полиномов с весом, равным плотности распределения случайных величин. Согласно теореме 3 для каждой плотности распределения существует единственная система ортонормированных полиномов. [38]
Интегрируя это выражение по аргументу Xi в бесконечных пределах, получим плотность распределения случайной величины Y ( см. § 3.5, гл. [39]
 |
Функция распределения случайной величины х. а - непрерывной. б - дискретной. [40] |
Таким образом, если нам удается определить функцию распределения или соответствующую ей плотность распределения случайной величины или, другими словами, определить закон распределения случайной величины, то мы получим самую полную вероятностную характеристику этой случайной величины. [41]
Если ф - функция немонотонная, то обратная функция неоднозначна, и плотность распределения случайной величины определяется в виде суммы стольких слагаемых, сколько значений ( при данном. [42]
Нахождение для каждой случайной величины системы полиномов, ортогональной с весом, равным плотности распределения случайной величины. Максимальная степень полинома в каждой системе должна равняться gz, z 1, I. [43]
Однако еще более интересно отметить, что в выражении (7.2) математическое ожидание от логарифмов плотностей распределения случайных величин X и 7 никакого отношения к закону информационно-сотового взаимодействия И. [44]
Таким образом, коэффициенты при ( - p) r / rl в разложении Тейлора преобразования Лапласа плотности распределения случайной величины х являются моментами порядка г этой величины. [45]
Страницы: 1 2 3 4
