Плотность - распределение - случайная величина
Cтраница 2
Эта функция называется плотностью распределения случайной величины X. [16]
Таким образом, зная плотность распределения случайной величины, мы можем определить вероятность того, что значение случайной величины попало в данный интервал. [17]
В формуле, описывающей плотность распределения случайной величины г, всего два параметра: среднее значение г и величина сигма о, определяющая разброс случайных значений г от своего среднего значения. Последняя величина в математической статистике называется относительным стандартным отклонением. [18]
Таким образом, зная плотность распределения случайной величины, мы можем определить вероятность того, что значение случайной величины попало в данный интервал. [19]
Таким образом, зная плотность распределения случайной величины, мы можем определить вероятность того, что значение случайной величины попало в данный интервал. [20]
Наиболее распространенным методом оценки плотности распределения случайной величины является построение ее гистограммы или полигона частот. С помощью группированных данных можно оценивать также моменты распределения, но при этом приходится вводить поправки на группировку. При использовании ЭВМ доступны и так называемые непараметрические оценки плотности, основанные на усреднении весов отдельных наблюдений, размазанных в окрестности каждого наблюдения, с помощью специально выбранной весовой функции. [21]
О построении доверительной области для плотности распределения случайной величины / Докл. [22]
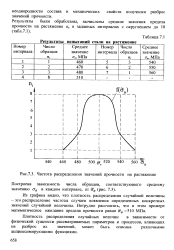 |
Результаты испытаний стали на растяжение. [23] |
Из графика видно, что плотность распределения случайной величины - это распределение частоты случаев появления определенных конкретных значений случайной величины. [24]
В табл. 8 приведены функции и плотности распределения случайных величин и параметры распределения этих законов, наиболее часто применяемых в практике расчетов процесса обводнения. В зависимости от степени неоднородности пластов по проницаемости, метода определения и получения информации о проницаемости фактическое ее распределение в лучшей степени описывается тем или иным теоретическим законом. [25]
В табл. 1.1 приведены функции и плотности распределения случайных величин и параметры распределения этих законов, наиболее часто применяемых в практике расчетов процесса обводнения. [26]
Заданная тем или иным способом зависимость плотности распределения случайной величины от ее конкретного значения называется законом распределения непрерывной случайной величины. [27]
Моменты случайных величин служат для описания свойств плотности распределения случайной величины J. Моменты содержат меньше информации о случайной величине по сравнению с плотностью распределения, но часто более удобны при решении прикладных задач. [28]
Если х распределена по нормальному закону, то плотность распределения случайной величины t зависит от числа выполненных измерений п и определяется формулой, в которую входят функции Г [ 4, стр. [29]
Поэтому wx ( и) обладает всеми свойствами плотности распределения случайной величины. [30]
Страницы: 1 2 3 4