Плотность - энергия - деформация
Cтраница 1
Плотность энергии деформации обратно пропорциональна расстоянию г от вершины трещины. [1]
 |
Локальная и глобальная система координат для определения стационарных значений. [2] |
Плотность энергии деформации изменяется от одного блока к другому. [3]
Плотность энергии деформации растет при приближении к краю трещины и на границе радиуса ядра трещины г0 достигает максимального значения. [4]
Плотность энергии деформации обратно пропорциональна расстоянию г от вершины трещины. [5]
Концепция плотности энергии деформации, Си [7] недавно предложил критерий разрушения, позволяющий рассчитать как предельные нагрузки, так и направление роста трещины. [6]
При этом выписанная плотность энергии деформации ( которую мы будем в дальнейшем называть и упругим потенциалом) должна быть функцией, симметричной по своим аргументам. [7]
 |
Микродилатация в элементе с мак-родисторсией ( / и микродисторсия в элементе с макродилатацией ( 2. [8] |
Таким образом, плотность энергии деформации включает энергию, идущую на дилатацию и дисторсию. Основные соотношения для каждого элемента могут различаться, поэтому решение увязывается с историей нагружения. [9]
При деформации рассматриваемого здесь вида плотность энергии деформации W для упругих материалов также является функцией параметров и и Я. При такой деформации сумма работ поверхностных усилий, распределенных по противолежащим граням, равна нулю, за исключением работы нормальных напряжений S3 на поверхностях z const и касательных напряжений S на поверхностях у - const. Очевидно, величина Я5 равна полному касательному усилию на поверхности, до деформации имеющей единичную площадь, a S3 / K представляет собой растягивающее напряжение, умноженное на площадь той грани, на которой оно действует. [10]
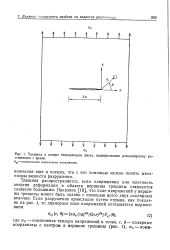 |
Трещина в центре бесконечного листа, подвергаемого равномерному растяжению с краев. [11] |
Трещина распространяется, если напряжения или плотность энергии деформации в области вершины трещины становятся слишком большими. Показано [16], что поле напряжений у вершины трещины может быть задано с помощью всего двух скалярных величин. [12]
Сложные подходы ( критического объема, плотности энергии деформации) аналитически представляются в наиболее общем виде. Они хорошо описывают результаты экспериментов на однонаправленных слоистых композитах с трещинами, ориентированными параллельно волокнам, и косоугольно армированных слоистых композитах, в которых процесс разрушения связан с образованием трещин в матрице. [13]
Сложные подходы ( критического объема, плотности энергии деформации) аналитически представляются в наиболее общем виде. Они хорошо описывают результаты экспериментов на однонаправленных слоистых композитах с трещинами, ориентированными параллельно волокнам, и косоугольно армированных слоистых композитах, в которых процесс разрушения связан с образованием трещин в матрице. [14]
Определенная так функция состояния имеет смысл плотности энергии деформации в геометрически нелинейной теории упругости. [15]
Страницы: 1 2 3 4