Кривая плотность - вероятность
Cтраница 1
Кривые плотности вероятности, получающиеся согласно формуле (3.175), еще более разнообразны по внешнему виду, чем графики распределения с функцией a ( t) или b ( t), взятых в отдельности. [1]
 |
Графики плотности вероятности ( а и функции распределения ( б нор. [2] |
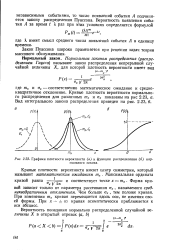
Кривые плотности вероятности нормального распределения для различных тх и ах показаны на рис 2.23, а. [3]
Теоретические кривые плотностей вероятностей распределения среднего числа отказов или наработки между отказами получаем в результате обработки гистограмм этих распределений, полученных на основании данных РИ. [4]
Вид кривых плотности вероятности ср ( /) для трех разных значений / приведен на рис. XIV. [5]
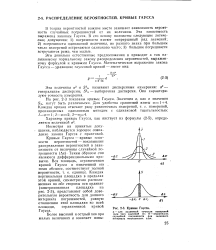 |
Кривые Гаусса. [6] |
Кривые Гаусса - кривые плотности вероятностей - показывают распределение вероятностей в зависимости от величины случайной погрешности ( Ал) - Таким образом они являются дифференциальными кривыми. Каждая вертикальная площадка в пределах этой кривой, симметрично расположенная по обе стороны оси ординат ( заштрихованная площадка на рис. 2 - 3), представляет собой доверительную вероятность для данного интервала погрешностей, равную отношению этой площадки ко всей площади, ограниченной кривой Гаусса. [7]
Если экстремум хХт кривой плотности вероятности дает минимум, то распределение называют антимодальным. [8]
Решение задачи нахождения кривой плотности вероятности является весьма желательным, но требует большого объема статистических исследований. [9]
На рис. 2.4 представлены кривые плотности вероятности разрушения, полученные методом ступенчатого повышения нагрузки при N 2 - Q5 и 107 по результатам испытаний соответственно 76 и 66 образцов. [10]
На рис. 5 представлены кривые плотности вероятности размеров диагоналей отпечатков алмазной пирамиды, изменение среднеквадратичного отклонения st и коэффициента вариации vt в зависимости от уровня нагрузки на индентор и размера диагонали, а также приведены кривые накопленной вероятности распределения размеров диагоналей отпечатков. Видно, что с ростом нагрузки рассеяние увеличивается и становится наиболее интенсивным при нагрузках от 50 до 100 гс. При дальнейшем увеличении нагрузки свыше 100 гс рост среднеквадратичного отклонения носит затухающий характер, стремясь к некоторому постоянному значению. Коэффициент вариации для полуциклов растяжения и сжатия ( соответственно светлые и темные точки на рис. 4а) уменьшается с ростом нагрузки по сравнению с его значениями при минимальной нагрузке на индентор, составляющей 10 гс, и, так же как среднее квадратическое отклонение, стремится, к некоторому предельному значению. Некоторое возрастание коэффициента вариации наблюдается при наиболее сильном росте среднего квадратичного отклонения в указанном выше диапазоне нагрузок на индентор. [11]
 |
Априорная плотность вероятности отказа. [12] |
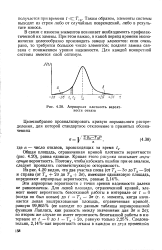
Общая площадь, ограниченная кривой плотности вероятности ( рис. 4.20), равна единице. Кривая этого рисунка описывает априорную вероятность. Поэтому, чтобь ( избежать ошибок при ее анализе, следует проявлять соответствующую осторожность. [13]
Величина Е характеризует крутость кривой плотности вероятности по сравнению с кривой Гаусса. [14]
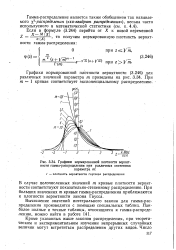 |
Графики нормированной плотности вероятности гамма-распределения при различных значениях параметра т. [15] |
Страницы: 1 2 3 4 5