Совместная плотность - вероятность
Cтраница 1
Совместные плотности вероятности ( 22) для многомерного случайного процесса подчиняются нормальному закону распределения. [1]
Совместная плотность вероятности р ( х, у) равна р ( х) р ( у х) и совместный ансамбль полностью определен. [2]
Совместные плотности вероятности ( 22) для многомерного случайного процесса подчиняются нормальному закону распределения. [3]
 |
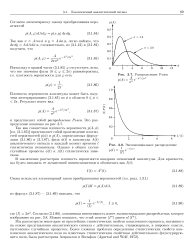
Приращение координаты броуновской частицы за время 2т равно сумме двух независимых приращений.. и.. [4] |
Совместная плотность вероятности представляет собой произведение двух плотностей вероятности для каждой из переменных по отдельности, поскольку эти два приращения статистически независимы. [5]
Совместная плотность вероятности р ( т, т ]) для значений T ] ( it) и г ] ( t) может быть найдена здесь следующим образом. [6]
Совокупность совместных плотностей вероятности обобщенных координат и скоростей исчерпывающе характеризует поведение механической системы при случайных воздействиях. [7]
 |
Распределение Рэлея.| Экспоненциальное распределение. [8] |
Так как совместная плотность вероятности р ( А, ф) [ см. (3.1.85) ] представляет собой произведение плотностей вероятностей р ( ф) и р ( А), определяемых формулами (3.1.86) и (3.1.87), фаза ф ( Ь и амплитуда A ( t) аналитического сигнала в каждый момент времени t статистически независимы. Однако в общем случае случайные процессы ф ( 1) и A ( t) статистически зависимы. [9]
В этом случае совместная плотность вероятностей для относительной диффузии является гауссовой. [10]
Какой вид имеет совместная плотность вероятности, если все переменные взаимно независимы. [11]
При определении такой совместной плотности вероятности возникают некоторые специфические трудности, однако будем полагать, что указанная совместная плотность вероятности известна. [12]
Отмеченная здесь структура совместной плотности вероятности некоррелированных нормальных величии имеет следующую аналогию. [13]
Отмеченная здесь структура совместной плотности вероятности некоррелированных гауссовских величин имеет следующую аналогию. [14]
Если принять, что совместная плотность вероятности системы функций Xj ( t) в каждый момент времени при стационарных колебаниях подчиняется нормальному закону распределения, то параметры этого закона распределения ( ах. [15]
Страницы: 1 2 3 4