Стационарная плотность - вероятность
Cтраница 1
Стационарная плотность вероятности ръ ( х) может быть, конечно, определена явно. [1]
Если стационарная плотность вероятности (6.44) не существует, то необходимо иметь в виду, что нуль - не только внутренняя граница, но и стационарная точка: при х О перенос и диффузия одновременно обращаются в нуль. Так как нуль - притягивающая точка, вся стационарная масса вероятности должна быть сосредоточена в нуле. [2]
Экстремумы стационарной плотности вероятности с этой точки зрения позволяют отслеживать такое качественное изменение. Число и положение экстремумов плотности вероятности ps ( x) в стохастическом случае и потенциала VK ( X) в детерминированном случае являются наиболее характерными отличительными особенностями стационарного поведения системы. [3]
Определяющей особенностью стационарной плотности вероятности влагозапасов бассейна Каспия и стока Волги является ее бимодальность. [4]
Таким образом, стационарная плотность вероятности речного стока при малых е и больших х асимптотически приближается к степенной функции. При очень больших значениях речного стока степенной закон плотности распределения вероятности сменяется гауссовским, так как при больших влагоза-пасах сток перестает зависеть от их величины и определяется только выпавшими осадками. Это обстоятельство приводит к тому, что степенной закон распределения плотности вероятности является промежуточной асимптотикой и неприменим в области очень больших значений увлажненности речных бассейнов. [5]
Хотя характер функциональной зависимости стационарной плотности вероятности от х изменяется при Ks a2 / 2 ( Ai cr2), это никак не сказывается на поведении среднего значения и дисперсии ( результат вполне предвидимый в свете сказанного в разд. Зависимость математического ожидания Е Х от X остается в точности такой же, как для устойчивого стационарного решения в детерминированной модели. В отличие от среднего значения и дисперсии экстремумы плотности вероятности позволяют обнаружить только вторую точку перехода, так как первая обусловлена изменением характера границы &i0, которая из притягивающей становится естественной. Это можно интерпретировать следующим образом: при О К сг2 / 2 флуктуации доминируют над автокаталитическим ростом популяции, и вымирание остается наиболее вероятным, но уже не достоверным исходом. Нельзя не заметить, что хотя в действительности численность популяции никогда не падает до нуля, поскольку граница b - Q естественная, тем не менее значительная доля вероятностей ма сы сосредоточена в исче-зающе малой окрестности нуля так, чте функция распределения Р ( х) выходит из нуля с вертикальной карательной. Таким образом, задаваемая выражением (6.43) вероятность вымирания популяции отлична от нуля. При Я сг2 / 2 автокаталитический рост берет верх над воздействием флуктуации. В окрестности нуля это проявляется в том, что вероятность вымирания популяции падает до нуля и функция распределения выходит из нуля с горизонтальной касательной. [6]
В дальнейшем мы определим стационарную плотность вероятности р ( х), которая характеризует стационарное поведение системы, находящейся под воздействием внешнего белого шума, и обсудим ее основные свойства. [7]
Таким образом, при а2 4 стационарная плотность вероятности имеет три экстремума, из которых хт - максимумы. [8]
Таким же способом может быть найдена и стационарная плотность вероятности. [9]
Данный метод позволяет находить в нелинейных системах одномерные стационарные плотности вероятности, а также решать задачи нелинейной фильтрации. Основные результаты теории фильтрации иллюстрируются выбором параметров фильтра системы фазовой автоподстройки частоты. [10]
Этот переход четко прослеживается в поведении экстремумов стационарной плотности вероятности PS () - Что же касается моментов, то по ним обнаружить переход невозможно. [11]
Более того, можно показать, что если стационарная плотность вероятности существует и диффузионный процесс Xt при / 0 начинается с нее, то Xt - эргодический процесс. [12]
Это качественное изменение наиболее непосредственно отражается в экстремумах стационарной плотности вероятности, за исключением того случая, когда переход обусловлен характером границы ( разд. [13]
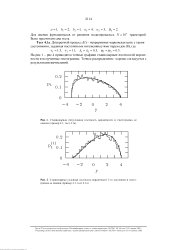 |
Стационарная безусловная плотность вероятности и гистограмма ее оценки ( пример, тест а.| Стационарная условная плотность вероятности 1-го состояния и гистограмма ее оценки ( пример, теет а. [14] |
На рис. 1 - рис. 4 приводятся точные графики стационарных плотностей вероятности и полученные гистограммы. Точное распределение хорошо согласуется с результатами вычислений. [15]
Страницы: 1 2 3 4