Стационарная плотность - вероятность
Cтраница 2
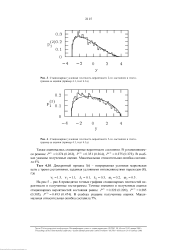
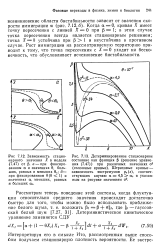
На рис. 5 - рис. 8 приводятся точные графики стационарных плотностей вероятности и полученные гистограммы. В скобках указаны полученные оценки. [17]
Более того, таким же способом может быть найдена и стационарная плотность вероятности. [18]
Результат (9.100) означает, кроме того, что при 0 стационарная плотность вероятности р ( х) имеет на критической линии А2 2у - 4 в дополнение к тройному экстремуму при х 1 / 2 еще по одному экстремуму слева и справа от критической точки, если точки х / 2 Ь лежат внутри носителя U. Поскольку это обстоятельство важно для всех корней уравнения (9.90), вычисленных посредством (9.96), получим теперь соответствующие условия. [19]
Интерпретируя его в смысле Ито, рассмотренным выше способом получаем стационарную плотность вероятности. [21]
В моделях, рассмотренных ранее, подобная процедура не нужна, поскольку стационарная плотность вероятности уменьшается по крайней мере экспоненциально всякий раз, когда оо является верхней границей пространства состояний. [22]
Это привело к неверному выводу о том, что равновесные уровни ( максимумы стационарной плотности вероятности уровня) расположены ниже уровня тяготения. С учетом / i 2 получается прямо противоположный результат: равновесные уровни на самом деле, как показал подробный анализ уравнений Фоккера-Планка - Колмо-горова и стохастического дифференциального уравнения водного баланса Каспийского моря (3.2.1), находятся выше уровня тяготения. Отметим, что решение линейного уравнения с мультипликативным внешним шумом, полученное в рассматриваемой статье, носит формальный характер, а методика, основанная на теореме Новикова, неприменима для нелинейной задачи, которая естественно возникает при корректном составлении уравнения водного баланса моря. [23]
Я) / ( Я) - 0 при Я - 0, то стационарная плотность вероятности нормируема. [24]
Как мы уже подчеркивали, в общем случае невозможно получить точное решение, например, для стационарной плотности вероятности системы, когда рассматривается шум произвольной формы. Дело обстоит так даже в довольно простом случае марковского гауссовского шума. Следовательно, общий случай внешнего цветного шума может быть рассмотрен лишь приближенными методами. Методы, развитые в гл. В частности, для последнего случая малых корреляционных времен в нашем распоряжении имеется метод разложения в ряд по теории возмущений. Этот метод использовался, чтобы показать, что фазовые переходы, индуцированные внешним шумом с малым временем корреляции, могут быть идентифицированы с переходами, исследованными в случае применения идеализации белого шума. Однако благодаря различию между двумя приближенными методами, используемыми для описания высокочастотного и низкочастотного шума, остается не ясным, каким образом переходы, предсказанные для случая быстрого шума, связаны с переходами, имеющими место в случае медленного внешнего шума. Желательно поэтому дополнить ту информацию, которая получается с помощью общих приближенных методов, информацией, полученной из изучения специальных классов внешнего цветного шума. Другими словами, полезно найти такие примеры Цветного шума, которые позволяют для произвольной системы с одной переменной точно вычислить по крайней мере стационарную плотность вероятности при любом значении времени корреляции. Как говорилось выше, гауссовский шум не принадлежит к этому классу. Следует обратиться к случайным процессам с более простой структурой, и вполне естественным кандидатом оказывается марковский процесс с дискретным пространством состояний. Простейшим процессом такого типа является дихотомический марковский шум, известный так же, как случайный телеграфный сигнал. В данной главе мы покажем, что он действительно позво ляет получить точные результаты и построить полную картину влияния корреляций. [25]
& покидают несущее множество р ( х) на одной и той же линии, где значение стационарной плотности вероятности изменяется от PS ( &. [26]
Как и в случае белого шума, модель Хонглера обладает критической точкой, индуцированной шумом, в которой стационарная плотность вероятности изменяет свой характер с одномодового на лвухмодовый. [27]
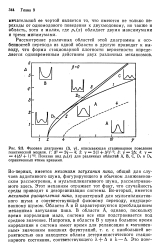
Рассмотрение различных областей этой диаграммы и особенностей перехода из одной области в другую приводит к выводу, что форма стационарной плотности вероятности определяется одновременным действием двух различных механизмов. [29]
Хотя при К а2 / 2 точка х О соответствует двойному экстремуму, характерная особенность критической точки ( скачкообразное изменение значения стационарной плотности вероятности ps) в большей мере напоминает ( жесткие) фазовые переходы первого рода. Такие переходы не сопровождаются критическим замедлением в классических ситуациях как равновесной, так и неравновесной. [30]
Страницы: 1 2 3 4