Апостериорная плотность

Cтраница 1

Апостериорная плотность по скорости формируется в этих условиях с помощью нескольких отсчетов положения движущихся объектов. [1]

Апостериорная плотность я ( 9 X) суммирует все знание о 9, содержащееся в наблюдениях X. Однако необходимо помнить, что бейесовская интерпретация v и т2 отличается от классической интерпретации. [2]

Таким образом, апостериорная плотность оцениваемого параметра зависит только от функции правдоподобия на п-м шаге wy ( zn - sn) и апостериорной плотности, найденной на предыдущем шаге. В этом нетрудно убедиться ( предоставляем читателю сделать это самостоятельно), если заметить что на каждом шаге апостериорная плотность гауссова, а оценка равна апостериорному среднему. Алгоритм обработки получается линейным и по структуре представляет собой дискретный фильтр Калмена. [3]

Оценки, соответствующие максимальной апостериорной плотности, обладают свойствами, схожими со свойствами оценок максимального правдоподобия, указанными в предыдущем разделе. [4]

Точность т - 2 апостериорной плотности равна сумме точностей априорной плотности и наблюдаемого среднего. [5]

Получение простого выражения для апостериорной плотности р ( Э) обычно требует тщательного выбора априорной плотности р ( 8), так называемой естественно сопряженной плотности. [6]

Однако именно из-за случайности п апостериорные плотности пп ( К), полученные в гипотетическом предположении наличия ровно п сигналов, оказываются непригодными. В прикладных задачах важно определить, какова вероятность наличия сигнала, параметр К которого лежит в данном интервале. Можно было бы сузить область Q до величины этого интервала, но тогда не была бы учтена априорная статистика взаимного расположения сигналов. К) входят в операторы оптимального обнаружения и измерения совокупности сигналов. [7]

Этот этап выполняется на основании найденной апостериорной плотности распределения р ( х у) и принятого критерия качества оценки. Примеры возможных критериев и соответствующие решения указаны выше. [8]

Чтобы и в рассматриваемом случае апостериорную плотность аппроксимировать гауссовским законом, функции / [0] и А [0] раскладывают, например, в ряд Тейлора. [9]

В данном разделе мы рассмотрим вычисление апостериорной плотности р ( 9) и требуемой плотности р ( х &) для случая, когда p ( x fi) - W ( ц 2), а вектор среднего значения ц есть неизвестный вектор параметров. [10]

Из (2.67) следует, что отношение апостериорной плотности параметра к априорной равно отношению функции правдоподобия к усредненной по параметру функции правдоподобия. [11]

Отметим в заключение, что построение точной апостериорной плотности распределения параметров 9 возможно только для линейно параметризованных моделей. Однако большинство моделей химико-технологических процессов являются нелинейно параметризованными. Поэтому для них обычно требуется линеаризация по параметрам. [12]

Желаемой характеристикой априорной плотности является то, что апостериорная плотность должна принадлежать тому же семейству. [13]

Заметим, что в том случае, когда апостериорная плотность существенно у ке, чем эффективная ширина Д функции вида (6.5.4), и ограниченные и неограниченные функции потерь будут приводить практически к одинаковым оценкам. [14]

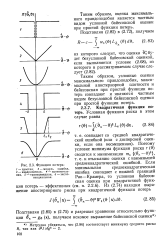Функция потерь. [15]

Страницы: 1 2 3 4