Поверхность - постоянная энергия
Cтраница 1
 |
Поверхности постоянной энергии для зон J 3 / 2 ( / s в полупроводниках типа алмаза и цинковой обманки. [1] |
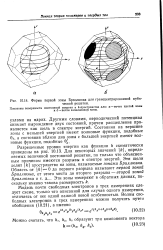
Поверхности постоянной энергии, описываемые выражениями ( 2.66 а) и (2.666), приведены на рис. 2.16. Форму этих поверхностей называют гофрированной сферой. В сущности, можно утверждать, что эти гофрированные сферы являются единственно возможными формами поверхностей постоянной энергии, описываемых в кубических кристаллах квадратным уравнением. Если пренебречь членами более высокого порядка, то наиболее общее выражение зависимости энергии от k для компоненты / g ( j 3 / 2) состояния Г в кубическом кристалле имеет вид (2.62), где А, В и С линейно независимые параметры, связанные с матричным элементом импульса электрона. Из определения коэффициентов А, В и С в (2.63) - (2.65) следует, что С может быть выражено через Лив. [2]
 |
Форма первой зоны Бриллюэна для гранецентрированной кубической решетки. [3] |
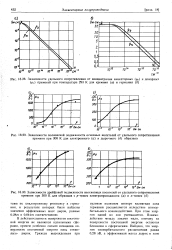
Показаны поверхности постоянной энергии в ft - пространстве для: а-почти пустой зоны и б-почти заполненной зоны. [4]
Если поверхности постоянной энергии электрона - сферы (1.204), то время релаксации тэ - скалярная величина, зависящая от модуля волнового вектора электрона. [5]
 |
Форма и расположение изоэнергетических поверхностей в Ge, Si и GaAs. [6] |
Форма поверхностей постоянной энергии показана на рис. 15.5. Для германия имеется восемь эллипсоидов, вытянутых вдоль осей 111, границы зоны Бриллюэна расположены в середине эллипсоидов. Для кремния имеется шесть эллипсоидов, вытянутых вдоль осей 100, центры эллипсоидов локализованы на расстоянии около трех четвертей от центра зоны Бриллюэна. Для арсенида галия поверхностями постоянной энергии являются сферы с центром в середине зоны Бриллюэна. [7]
 |
Полупроводниковые соединения A11. [8] |
Вблизи него поверхность постоянной энергии близка к эллипсоиду вращения с большой осью, направленной вдоль оси а. Экстремум валентной зоны расположен в точке k O. [9]
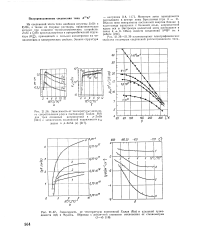 |
Зависимость от температуры постоянной Холла R ( a и удельной проводимости о ( б в MgsSba. Образцы с различной степенью отклонения от стехиометрии. [10] |
Вблизи него поверхность постоянной энергии близка к эллипсоиду вращения с большой осью, направленной вдоль оси а. [11]
В действительности поверхности постоянной энергии не являются идеальными сферами, причем особенно сильно искажена поверхность постоянной энергии зоны тяжелых дырок. [13]
XN называют поверхностью постоянной энергии для данного движения. [14]
Предположим, что поверхность постоянной энергии является компактом и достаточно регулярна, так что применима элементарная теория поверхностных интегралов. [15]
Страницы: 1 2 3 4