Поверхность - постоянная энергия
Cтраница 2
Поверхностью Ферми называется поверхность постоянной энергии в трехмерном k - пространстве, которой соответствуют состояния с энергией, равной энергии Ферми при 0 К. Представляется интересным построить такую поверхность исходя из зависимости энергии от вектора k, найденной в разд. [16]
Предположим, что поверхность постоянной энергии является компактом и достаточно регулярна, так что применима элементарная теория поверхностных интегралов. [17]
Поверхностью Ферми называется поверхность постоянной энергии в трехмерном k - пространстве, которой соответствуют состояния с энергией, равной энергии Ферми при 0 К, Представляется интересным построить такую поверхность исходя из зависимости энергии от вектора k, найденной в разд. [18]
Его ограничение на поверхности постоянной энергии Н const, по которым происходит классическое движение, играет большую роль при статистическом описании классической системы, когда фазовый объем области пропорционален вероятности пребывания в ней состояния системы. Эта роль фазового объема сохраняется в КТП, где при вычислении вероятности переходов из начального состояния рассеяния в конечное ( скажем, системы плоских волн), классические степени свободы входят в эту вероятность в виде множителя, пропорционального фазовому объему конечных состояний. [19]
Заметим, что поверхности постоянной энергии для валентных зон, определенные формулой (2.62), обладают инверсионной симметрией: E ( k) E ( - k) хотя кристалл может и не обладать такой симметрией. Если гамильтониан инвариантен при обращении времени, эти две блоховские волны будут иметь одинаковые энергии. [20]
Рассмотрим теперь на поверхности постоянной энергии активной молекулы H ( pi, qi) Eo некоторую траекторию, приводящую к реакции. Элемент гиперповерхности ds можно представить в виде dtyda, где city - элементарный интервал времени между двумя точками, движущимися вдоль выбранной траектории, da - нормальный к траектории элемент гиперповерхности с размерностью на единицу меньше. Поскольку интервал dty остается постоянным вдоль траектории, а элемент гиперобъема dw сохраняется в силу теоремы Лиувилля, величина da также остается неизменной. [21]
На самом деле поверхности постоянной энергии не являются идеальными сферами, причем особенно сильно искажена поверхность постоянной энергии зоны тяжелых дырок. Трижды вырожденная при нулевом волновом векторе валентная зона германия расщепляется вследствие спин-орбитального взаимодействия. При этом энергия одной из зон уменьшается. Взаимодействие отщепившейся зоны с остальными зонами мало, поэтому их поверхности постоянной энергии остаются близкими к сферическим. [22]
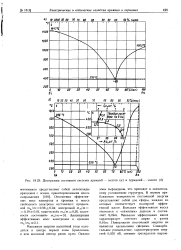 |
Диаграмма состояния системы кремний-золото ( а и германий - золото ( б. [23] |
В первом приближении поверхности постоянной энергии представляют собой две сферы, каждая из которых соответствует скалярной эффективной массе. Поверхности постоянной энергии не являются идеальными сферами. [24]
Более точный учет несферичности поверхностей постоянной энергии приводит лишь к несущественным поправкам к этим формулам. [25]
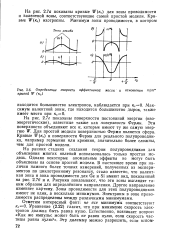 |
Определение скорости эффективной массы и отношения m / m кривой W ( кс. [26] |
На рис. 2.7 г показаны поверхности постоянной энергии ( изо-знергетические), известные также как поверхности Ферми. Эти поверхности объединяют все к, которые имеют ту же самую энергию W. Для простой модели поверхностью Ферми является сфера. Кривые W ( KC) и поверхности Ферми для реального полупроводника, например германия или кремния, значительно более сложны, чем для простой модели. [27]
Интегрирование в (2.99) проводится по поверхности постоянной энергии Ув Е, dy - элемент этой поверхности, q, р - координаты и импульсы. [28]
Итак, мы рассматриваем одну поверхность Q постоянной энергии, на которой задан второй интеграл. [29]
Сфера в подпространстве ур является поверхностью постоянной энергии. [30]
Страницы: 1 2 3 4