Энергетическая поверхность
Cтраница 1
 |
Схема энергетического. [1] |
Энергетическая поверхность имеет две долины, разделенные как бы горным хребтом с перевалом на нем, представляющим собой седловин-ную точку. Правый нижний участок поверхности ( около абсцисс 2 0 - 2 2) отвечает состоянию, при котором атом С находится на. АВ и взаимодействие между ними еще мало. [2]
Хартрп-фоковская энергетическая поверхность параллельна в этих областях точной энергетической поверхности. На больших расстояниях между взаимодействующими объектами такое удачное поведение уже но имеет места. [3]
Энергетическая поверхность пары молекул С и D переходит без разрывов в поверхность А и В, так как обе пары молекул построены из одних и тех же атомов. В общем случае две области ( А - - В) и C - - D) разделены энергетическим барьером, через который должна перейти исходная система ( Л - J - В) для того, чтобы произошла реакция. Плато с одной стороны барьера соответствует состоянию, в котором система состоит из молекул Л и В; плато с другой стороны барьера отвечает системе из молекул С и D. Плато слева и справа от потенциального барьера соответствуют конфигурациям а и Ь в примере реакции изомеризации, описанной в предыдущем разделе. При перемещении от одного плато к другому система обычно проходит через самый низкий перевал энергетического барьера. Обычно скорости протекания этих реакций зависят в основном от их энергий активации. [4]
Если энергетические поверхности в случае Д рассчитывались в упомянутых выше работах методом атом-атомных потенциалов, то в ситуации X интересные результаты были получены квантово-химическим расчетом. [5]
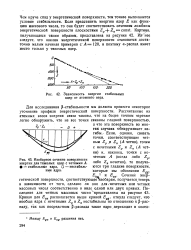 |
Зависимость энергии стабильных ядер от атомного веса.| Изобарное сечение поверхности энергии для тяжелых ядер с четными А. - стабильные ядра, О - нестабильные ядра. [6] |
Сечение энергетической поверхности, соответствующее изобарам, получаетсядеперь в зависимости от того, сделано ли оно дляснечетных или четных массовых чисел соответственно в виде одной или двух кривых. [7]
Расположение энергетических поверхностей в двумерном случае может существенно отличаться от одномерного случая. Снабдим их нижними индексами h и d, а также 1 и 2 для первой и второй зон. Тогда в двумерном случае возможно ( но не обязательно. Поэтому по энергии вторая зона как бы заходит за первую и на ординате не получается запретного интервала энергии. В одномерном случае это невозможно. Показанное на рисунке 57 расположение энергетических поверхностей в двух зонах Бриллюэна называется перекрытием зон. Аналогичное расположение, очевидно, может осуществляться и в трехмерном случае. [8]
 |
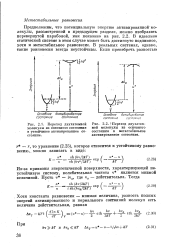
Переход двухатомной молекулы из основного состояния в устойчивое активированное состояние.| Переход двухатомной молекулы из основного состояния в метастабильное активированное состояние. [9] |
Из-за кривизны энергетической поверхности, характеризующей неустойчивую систему, колебательная частота v является мнимой величиной. [10]
При рассмотрении энергетической поверхности мы убедились в том, что при данном нечетном А в ряду изобар может быть только один стабильный нуклид. При четных А может быть до трех четно-четных изобар, стабильных по отношению к р-распаду, приводящему к образованиям их нечетно-нечетных соседей. Поскольку двойной 3-распад, если он существует, является крайне маловероятным процессом ( t / a 1016 лет), то такие ядра можно считать вообще стабильными по отношению к 3-распаду. [11]
 |
Переход двухатомной молекулы из основного состояния в устойчивое активированное состояние. [12] |
Из-за кривизны энергетической поверхности, характеризующей неустойчивую систему, колебательная частота v является мнимой величиной. [13]
 |
Энергетический слой в Г - пространстве. Область из допустимых. [14] |
Свойства симметрии энергетической поверхности следуют из обратимости ( относительно времени) орбит, порождающих поверхность х) ( см. гл. [15]
Страницы: 1 2 3 4