Энергетическая поверхность

Cтраница 4

Как мы уже отмечали, все члены, которые содержат Г - матрицы вне энергетической поверхности и происходят от различных слагаемых (7.110), взаимно уничтожаются. [46]

Напомним только, что решение этой задачи для трехмерного случая приводит обычно к сложным, изогнутым энергетическим поверхностям в пространстве импульсовг или волновых чисел. [47]

Ввиду квазиоднородности гамильтониана (3.10) точно такая же картина трансверсальных сепаратрис имеется на всех энергетических поверхностях с положительным значением полной энергии. В качестве следствия получаем, что уравнения (3.11) не имеют дополнительного аналитического интеграла. Этот результат был получен ранее в работе С. Л. Зиглина [64] с использованием анализа ветвления решений системы (3.11) в плоскости комплексного времени. [48]

Соотношения (7.15), (7.16), (7.17) определяют матричные элементы для парциальной волновой - матрицы на энергетической поверхности. [49]

Мы рассмотрели до сих пор только те реакции, которые происходят на одной и той же энергетической поверхности. Часто, однако, две такие поверхности подходят очень близко друг к другу или даже как будто пересекаются. [50]

В случае рассеяния простейший подход состоит в том, чтобы использовать значения k k k на энергетической поверхности. [51]

Квазиэргодичность системы не предполагает, что фазовая траектория за время т - - оо покроет всю энергетическую поверхность; некоторая неоднородность р сохраняется. [52]

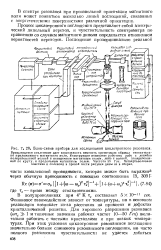Блок-схема прибора для исследования циклотронного резонанса. [53]

В спектре резонанса при произвольной ориентации магнитного поля может появиться несколько линий поглощений, связанных с энергетическими поверхностями различной ориентации. [54]

Пуанкаре доказал, что единственной поверхностью, которую точка системы не покидает при своем движении, является энергетическая поверхность. Он показал, что если динамическая траектория системы не сходит с поверхности, то такая поверхность может быть только энергетической. Ферми обобщил эти результаты и доказал, что для систем, которые он назвал Kanonische Nor-malsysteme, не существует никаких других однозначно определенных стационарных аналитических интегралов, кроме интеграла энергии. [55]

Как и всякий элементарный акт химического превращения, элементарный акт катализа в общем случае можно описать с помощью потенциальной энергетической поверхности, которая однозначно характеризует структуру системы и дает наиболее полные сведения об элементарном акте. Эти квантовомеханические данные имеют то преимущество, что все вопросы здесь решают с единой точки зрения и геометрические параметры системы находят из общих энергетических соображений. Однако решение уравнения Шредингера для мультиплетной адсорбции и каталитического превращения является задачей такой трудности, что даже качественное ее рассмотрение пока неосуществимо. Поэтому приходится искать приближенные методы, в которых геометрические и энергетические параметры рассматривают раздельно, но вместо единого описания, дающего необходимые и достаточные условия каталитического превращения, здесь возникают как бы независимые принципы геометрического и энергетического соответствия, которые в теории муль-типлетов Баландина рассматриваются как два условия, каждое из которых хотя и необходимо, но не является достаточным для катализа. [56]

Страницы: 1 2 3 4