Поворот - координатная ось
Cтраница 2
Выбор знака определим условием: поворот вокруг координатной оси на положительный угол должен осуществляться против часовой стрелки, если смотреть на него со стороны положительного направления оси. [16]
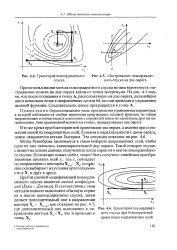 |
Траектория покоординатного [ IMAGE ] Застревание покоординат-спуска ного спуска на дне оврага.| Траектория покоординатного спуска при благоприятной ориентации координатных осей. [17] |
Метод Розенброка заключается в таком повороте координатных осей, чтобы одна из них оказалась квазипараллельной дну оврага. Такой поворот осуществляют на основе данных, полученных после серии из п шагов покоординатного спуска. Xt n - Хк; остальные оси выбирают из условия ортогональности к X, и друг к другу. [18]
Рассмотрим отдельно перенос начала координат и поворот координатных осей. [19]
Значения а0 и а инвариантны к повороту координатных осей. [20]
Компоненты любого такого вектора преобразуются при поворотах координатных осей по таким же формулам, как и координаты. [21]
Покажем прежде всего, что при помощи поворота координатных осей его всегда можно привести к виду, не содержащему члена с произведением переменных. [22]
Из аналитической геометрии известно, что путем поворота координатных осей уравнение поверхности второго порядка (1.23) можно преобразовать так, чтобы в новой координатной системе ( и, v, w) исчезли члены, содержащие произведения координат. [23]
Таким образом, из двенадцати возможных последовательностей поворотов вокруг координатных осей существенно различными являются лишь четыре. Последовательности из I и II класса называются углами конечного вращения первого рода. [24]
Тензор, компоненты которого не изменяются при повороте координатных осей, называется изотропным тензором. [25]
Этим доказана инвариантность s и S при поворотах координатных осей. [26]
Этим доказана инвариантность s и 6 при поворотах координатных осей. Аналогично, можно доказать и инвариантность определителя А. [27]
Второй цикл спусков и все последующие осуществляются после поворота координатных осей. [28]
В § 25 было показано, что преобразование поворота координатных осей относится к классу унитарных преобразований. Формулы (30.37) и (30.38) выражают унитарные преобразования операторов. Но представляет интерес найти соответствующее унитарное преобразование самих волновых функций. [29]
 |
Сопряженные направления жение из точки при поиске экстремума двумерной квадратичной функции. [30] |
Страницы: 1 2 3 4