Поворот - координатная ось
Cтраница 3
В я-мерной задаче с квадратичной целевой функцией после поворота координатных осей экстремум может быть найден за п одномерных поисков. [31]
Если мы совершенно произвольно условимся всегда связывать с пространственным поворотом координатных осей 5, описываемым формулой (15.32), преобразование (15.30) базисных состояний, которому отвечает матрица R в формулах (15.34), совпадающая с матрицей поворота 5, то в этом и только в этом случае числа gqa ( и aqa) будут преобразовываться как компоненты тензоров. [32]
Таким образом, сумма осевых моментов инерции при повороте координатных осей не изменяется, т.е. является инвариантом. [33]
Преобразование (96.1) к новым квантовым числам состоит в повороте координатных осей на 45; как видно из рисунка, квантовые числа / и m vie будут теперь меняться независимым образом. [34]
Это свойство напоминает инвариантность известной квадратичной формы при повороте координатных осей в трехмерном пространстве. [35]
Величина центробежного момента инерции непрерывно изменяется с изменением угла поворота координатных осей. При повороте осей на 90 величина центробежного момента меняет знак; следовательно, при переходе от одного знака к противоположному должно быть и такое положение осей, для которого она будет равна нулю. [36]
Это достигается переносом начала координат в точку оптимума и поворотом координатных осей. [37]
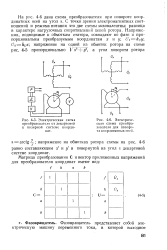 |
Электрическая схема преобразователя от декартовой к полярной системе координат.| Электрическая схема преобразователя для поворота координатных осей. [38] |
На рис. 4 - 6 дана схема преобразователя при повороте координатных осей на угол а. С точки зрения электромагнитных соотношений и режима питания эти две схемы эквивалентны; разница в характере нагрузочных сопротивлений цепей ротора. [39]
Исходя из закона преобразования компонент вектора как объекта, не зависящего от поворота координатных осей, вытекает его определение. [40]
Таким образом, всегда можно выбрать угол а так, что после поворота координатных осей на этот угол в уравнении линии 2-го порядка исчезнет член с произведением переменных. [41]
Согласно более строгому определению вектором называется совокупность трех величин, преобразующихся при поворотах координатных осей по определенному закону. [42]
Таким образом, матрица направляющих косинусов однозначно определяет формулы преобразования координат при повороте координатных осей. [43]
Так же, как и в двух предыдущих системах, в прямоугольной системе трудно осуществлять поворот координатных осей, например учитывать качку корабля. По упрежденным значениям прямоугольных координат трудно вычислять баллистические величины. Кроме того, эта система не содержит азимута, необходимого для горизонтального наведения орудия или пусковой установки. Все это приводит к необходимости после решения задачи встречи вновь пересчитывать координаты. [44]
И) системе определяется уравнениями прсобразова-ния декартовых прямоугольных координат, в общем случае переноса и поворота координатных осей; в частном случае - только поворота осей, если начала локальных систем координат совпадают. [45]
Страницы: 1 2 3 4