Подсистема - уравнение
Cтраница 1
Подсистема уравнений ( 2) в симплексе реакции имеет, по крайней иере, одну стационарную точку. [1]
Строго соподчиненными подсистемами уравнений называют такие подсистемы, которые можно решить в отдельности в определенном последовательном порядке. Эти подсистемы не содержат взаимосвязанных уравнений, решаемых совместно друг с другом. [2]
Выделение подсистемы уравнений путем исключения уравнения движения, как это принято в большинстве моделей, сближает расчет на устойчивость с динамическими расчетами ( см. гл. [3]
Выделим подсистему Sj уравнений, каждое из которых содержит EJ. Пусть выделенные уравнения содержат другие неизвестные не более одного раза, т.е. ортогональны. [4]
При этом подсистема уравнений количества движения и баланса массы газа решается на аналоге, а подсистема уравнений баланса энергии и состояния - на цифровом автомате. [5]
К настоящему моменту подсистема уравнений (1.4) - (1.18) удовлетворена, и равенства (1.29) представляют ее общий интеграл. [6]
В результате решения выделенной подсистемы уравнений определяются значения параметров потока во времени и по длине парогенерирующего канала при нанесении какого-либо возмущения. [7]
Уравнение (13.6) является следствием подсистемы уравнений второго закона Кирхгофа ( см. об этом в [167], а также в гл. Предполагается также, что энергия источника полностью тратится на преодоление трения в сети, т.е. не учитывается энергия, доставляемая потребителям. Такое допущение приемлемо для многих схемно-структур-ных задач. [8]
Эти модели должны содержать: подсистемы уравнений для ветвей, которые с заданным приближением будут отражать фактическое изменение параметров состояния транспортируемой среды, а также и сетевые уравнения, отвечающие за совпадение граничных значений этих параметров на концах ветвей для цепи в целом в соответствии с ее схемой и законами сохранения. С математической точки зрения это приводит в общем случае к специальному классу смешанных систем уравнений, включающих замыкающие уравнения в дифференциальной или интегральной формах, а также и в частных производных, если это необходимо. [9]
Граничные условия, через которые связываются подсистемы уравнений обеих фаз в (5.5.31), заданы на подвижной границе. [10]
Иногда появляется возможность выделить из исходной системы уравнений т непересекающихся подсистем уравнений, в каждой подсистеме ti уравнений, s неизвестных. [11]
При явной декомпозиции система ( 1 - 2) делится на п подсистем уравнений с собственными критериями / ор; выходные координаты каждой подсистемы хр полагаются равными некоторым заданиям Яр. Задача оптимизации р-той подсистемы заключается в нахождении такого вектора мр, чтобы функция / ор достигала максимума при выполнении соответствующих связей модели ( 1 - 2), части ограничений ( 1 - 8), ( 1 - 8а) и дополнительного условия Хр Яр. Центральная задача заключается в нахождении величин Яр, доставляющих максимум критерию / 0 при выполнении ограничений на Яр или, точнее, на координаты хр. [12]
Отличительная особенность диакоптическнх методов анализа - возможность организации независимых вычислительных процессов отдельно для каждой подсистемы уравнений. Но для получения достоверных результатов нужно учитывать взаимовлияние подсистем. Поэтому в диакоптических методах периодически проводится согласование результатов вычислений в независимых подсистемах. Применительно к моделям макроуровня это согласование может производиться после ( или в ходе) выполнения: а) серии исключений неизвестных при решении ЛАУ методом Гаусса; б) серии итераций при решении систем нелинейных АУ; в) серии шагов интегрирования ОДУ. Соответственно различают три группы диакоптических методов. [13]
При этом подсистема уравнений количества движения и баланса массы газа решается на аналоге, а подсистема уравнений баланса энергии и состояния - на цифровом автомате. [14]
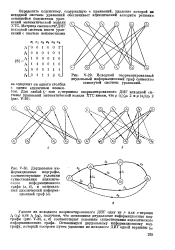 |
Двудольные информационные подграфы, соответствующие условиям существования ациклического информационного графа ( а, б, и оптимальный циклический информационный граф ( в. [15] |
Страницы: 1 2 3 4