Макроскопический подход
Cтраница 3
 |
Схема деформаций кристалла при скольжении ( а ] и двойииковаики ( б. ПС-плоскость скольжения. ПД - - плоскость двойнккования. [31] |
Процессы деформации и разрушения тела при нагруженни изучают не только с позиций, основанных на дискретном строении тела, но и на основе макроскопического подхода, связанного с представлением твердого тела в виде области, заполненной непрерывной сплошной средой. [32]
Процессы деформации и разрушения тела при нагружении изучают не только с позиций, основанных на дискретном строении тела, но и на основе макроскопического подхода, связанного с представлением твердого тела в виде области, заполненной непрерывной сплошной средой. Если изучение деформации и разрушения твердого тела с микроскопических позиций основано на анализе искажений кристаллической решетки и соответствующих им напряжений, вызванных действием на тело внешних силовых факторов, то с позиций механики континуума движение частиц тела определяется в большей степени физическим и механическим поведением среды. При этом модель твердого тела может быть представлена сплошной средой с определенными физико-механическими свойствами. [33]
Стремление к углубленному рассмотрению внутренних процессов в действительных средах, включая сюда процессы переноса, приводит во многих случаях к необходимости отказа от макроскопического подхода механики сплошных сред в пользу микроскопических методов статистической механики, позволяющих значительно ближе подойти к выяснению природы скрытых молекулярных процессов и разнообразных форм движения материи. Уравнения статистической механики значительно сложнее уравнений механики сплошных сред, хотя и аналогичны им по типу, и также требуют дополнительных допущений при решении конкретных задач. [34]
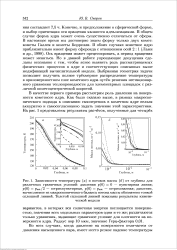
Отметим, что результаты измерения поляризуемости кластеров натрия ag ненамного превышают поляризуемость R идеально проводящей сферы соответствующего радиуса Rg [27], что также свидетельствует в пользу применимости макроскопического подхода. [35]
При микроскопическом описании никаких соотношений вводить не нужно; единственная неизвестная / уже содержит всю информацию о плотности, скорости, температуре, напряжениях и тепловом потоке. Макроскопический подход ( 5 функций от 4 переменных) проще микроскопического ( 1 функция от 7 переменных), и, если только он возможен, его следует предпочесть, Таким образом, одна из задач теории, основанной на уравнении Больцмана, состоит в выводе для газа при: обычных условиях некоторой приближенной макроскопической модели и в отыскании пределов применимости этой модели. [36]
До сих пор энергия электростатического взаимодействия заряженных поверхностей раздела рассчитывалась в предположении, что заряд распределен по поверхности равномерно, со средней плотностью а. Такой макроскопический подход оправдан, когда толщина h слоя электролита ( зазора) существенно превосходит характерное расстояние / между зарядами на поверхности раздела. При этом электростатическое расклинивающее давление полностью определяется концентрацией и типом электролита, его температурой и величиной макроскопического электростатического потенциала Фш в плоскости симметрии. Потенциал в объеме электролита, с которым рассматриваемый слой находится в контакте, предполагается равным нулю. [37]
При макроскопическом подходе достаточно ограничиться непосредственно наблюдаемыми энергетическими процессами, не принимая во внимание механизма этих процессов. Именно таким путем идет термодинамика, которая обеспечивает теоретическую основу при разработке тепловых двигателей. Для определенного уровня практических требований такой подход вполне удовлетворителен. [38]
Здесь буду 1 рассмотрены макроскопические подходы к этой проблеме, основанные на различных моделях разрушения ( вязкое, хрупкое, смешанное), и некоторые общие теории. Реальные процессы разрушения материалов настолько сложны, что указанные модели могут рассматриваться лишь как первое приближение. Поэтому на полученные с ломощью этих моделей формулы следует смотреть как на приближенные. Вследствие этого теоретические исследования длительной прочности на основе указанных моделей имеют большое значение и перспективу развития. [39]
К сожалению, прямое численное моделирование турбулентных течений на основе точных ( мгновенных) гидродинамических уравнений сопряжено с большими математическими трудностями, а построение общей теории турбулентности из-за сложности механизмов возникновения и эволюции взаимодействующих когерентных структур вряд ли возможно. Это приводит к необходимости развития новых оригинальных макроскопических подходов к описанию турбулентности, введения адекватных физических параметров среды, установления универсальных и частных соотношений для их определения, дополняющих известные соотношения типа законов сохранения массы, энергии, количества движения и др. В работе проф. [40]
В феноменологической неравновесной термодинамике [70] используется чисто макроскопический подход, основанный на локальных уравнениях состояния и линейных соотношениях между неравновесными потоками и так называемыми термодинамическим силами. В неравновесной термодинамике они являются заданными величинами и берутся из эксперимента. [41]
Первая часть курса Основы инженерной электрофизики посвящена взаимодействию электромагнитных волн с веществом. Рассмотрение ограничено в большинстве случаев тем макроскопическим подходом, который необходим для понимания принципов работы вычислительных, измерительных и кибернетических устройств - как современных, так и находящихся в стадии исследования и разработки. [42]
Как было сказано выше, в рамках макроскопического подхода к описанию газопереноса в кометном ядре нельзя аккуратно и самосогласованно задать значение этой характеристики. [44]
Рассмотрим теперь подробнее магнитный момент электрона, его поведение в магнитном поле и условия, при которых магнитные моменты электронов в атоме компенсируют друг друга. Понятие о магнитном моменте, которое при макроскопическом подходе можно ввести, рассматривая свойства контура с током в магнитном поле, в атомной физике вводится с помощью представления о так называемом атомном токе. Поскольку электроны, движущиеся в атоме вокруг ядра, обладают электрическим зарядом, они создают замкнутый ток, которому, по аналогии с макроскопическими токами, приписывается магнитный дипольный момент. Этот момент тесно связан с механическим моментом количества движения, так как электрон обладает не только зарядом, но и массой. [45]
Страницы: 1 2 3 4