Макроскопический подход

Cтраница 2

Ниже мы используем макроскопический подход к построению модели усталостного разрушения поверхности, который, как известно ( см. [70, 83]), состоит в построении положительной неубывающей во времени функции Q ( M, i), характеризующей меру повреждения материала в точке М и зависящей от амплитудных значений напряжений в данной точке. Такой подход применим к исследованию как поверхностного разрушения, так и разрушения внутри тела. Кроме того, в [91] показано, что параметры объемного и поверхностного усталостного разрушения для ряда материалов ( например, для некоторых видов резин) совпадают. [16]

С точки зрения макроскопического подхода к распространению усталостной трещины процесс повреждения характеризуется скоростью распространения усталостной трещины. Сделаны попытки выразить ее в аналитической форме с помощью свойства материала и параметров нагружения. [17]

Данная глава ограничивается макроскопическим подходом к кинетике реакций. При исследованиях химической микрокинетики используются более сложные численные методы для оценки межмолекулярных взаимодействий статистическими методами или посредством квантовой механики, что не входит в рамки данной главы. [18]

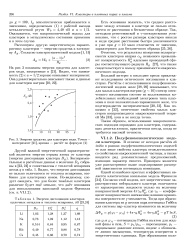Энергии сродства для кластеров меди. Точки - эксперимент, кривая - расчет по формуле ( 2.| Энергии диссоциации кластеров щелочных металлов и теплоты испарения, эВ. [19]

Таким образом, использование макроскопических подходов оправдано для кластеров, содержащих десятки атомов, практически всегда, когда не требуется высокой точности. [20]

Как мы уже говорили, макроскопический подход к исследованию химической энергии вполне удовлетворителен при решении большинства практических задач сегодняшнего дня. Однако для полного и глубокого изучения природы химических связей необходимо рассмотреть строение атома, поскольку именно от структурных особенностей атомов зависит, возникнет ли при их столкновении притяжение или будут преобладать силы отталкивания, и атомы разлетятся в неизмененном состоянии. Квантовая теория, изучающая строение атома, уже объяснила многие вопросы химической связи. Изложение квантовой теории выходит за рамки этой книги, поэтому мы ограничимся лишь несколькими замечаниями. [21]

Ими было рассмотрено соответствие между микроскопическим и макроскопическим подходом в теории разрушения. [22]

Метод контрольного объема основан на применении макроскопического подхода к описанию физических явлений. Это особенно важно, когда дифференциальные уравнения не всюду имеют непрерывные решения, которые можно было бы в каждой точке представить рядами Тейлора. Однако в рассмотренных задачах не существует решений с разрывами. [23]

Оценки значений величины Г в рамках макроскопического подхода были выполнены в гл. [24]

Для того чтобы обосновать правомерность такого макроскопического подхода, рассмотрим кинетику поглощения вещества в некотором объеме F, малом относительно габаритов прибора, в котором помещен зерненый материал, и большом относительно размеров зерен. [25]

Для анализа напряжений в композитных плитах обычно применяется макроскопический подход, в котором считается, что каждый слой, состоящий из волокон и матрицы, представляет собой однородную среду, идеально связанную с примыкающими слоями. [26]

Следует, впрочем, отметить, что в силу макроскопического подхода, применяемого в теории Онзагера - Кирквуда - Фрелиха, указанная выше модель диэлектрика не является слишком грубой ( см. [18, 7]), а упрощения при выводе формулы ( 3 1) не существенны при описании свойств диэлектрика в области слабых полей. [27]

Для легких ядер ( R - - б) такой макроскопический подход не годится. Как показано в [25], в этом случае пионная неустойчивость ( как функция плотности нуклонов) наступает сначала для состояний с нулевым угловым моментом. При вычислении поляризационного оператора пионов, вместо интегрирования по импульсам нуклонных состояний ( как это делалось в бесконечной системе), производилось суммирование по квантовым числам нуклона в сферическом ядре и определялось значение константы gf gc, при котором наступает неустойчивость. В средних и тяжелых ядрах получаются приблизительно те же значения ge, что и в бесконечной системе. [28]

Вместе с тем, приведенные результаты Колмогорова-Обухова феноменологического моделирования мелкомасштабной структуры турбулентности позволяют пересмотреть макроскопические подходы к описанию развитой турбулентности, в частности, термодинамические методы, используемые при построении полуэмпирических моделей для одноточечных моментов. При этом теория Колмогорова-Обухова в полуэмпирических моделях турбулентности до последнего времени никак не применялась. Однако введение в гидродинамическую модель внутренних параметров среды, характеризующих возбуждаемые макроскопические степени свободы, дает возможность описать методами статистической неравновесной термодинамики колмогоровский каскадный процесс ( стационарно-неравновесный процесс), использовать в уравнениях движения в качестве индикатора перемежаемости зависящий от глобального числа Рейнольдса Re параметр Колмогорова ( ev), и получить разнообразные кинетические уравнения типа Фок-кера - Планка ( в соответствующем конфигурационном пространстве) для функций распределения важных характеристик мелкомасштабной турбулентности. [29]

В противоположность применявшемуся ранее микроскопическому подходу, основанному на рассмотрении взаимодействий молекул, был применен макроскопический подход, в котором взаимодействующие тела рассматривались как сплошные среды. [30]

Страницы: 1 2 3 4