Закон - плоское сечение
Cтраница 1
Закон плоских сечений существенно упрощает как постановку и решение задач сверхзвуковой аэродинамики, так и методы экспериментального исследования движения тел. [1]
Закон плоских сечений справедлив для всех балок и стержней независимо от физико-механических свойств материала. [2]
 |
Схема к объяснению закона плоских сечений. [3] |
Из закона плоских сечений следует закон подобия при гиперзвуковом обтекании тонких тел, к-рып позволяет, напр. [4]
Это есть закон плоских сечений, который играет фундаментальную роль в газовой динамике. [5]
Исходя из закона плоских сечений, вывести формулы метода упругих решений для случая, когда в сечении бруса возникают одновременно два изгибающих момента ( Мх и Му относительно первой и второй главных осей сечения) и продольная сила. [6]
Считаем, что закон плоских сечений имеет место и при изгибе кривых брусьев. [7]
Таким образом, закон плоских сечений для нестационарного обтекания тел позволяет заменить решение исходной задачи совокупностью решений задач меньшей размерности. [8]
Известно, что закон плоских сечений является следствием геометрических свойств стержня ( большая протяженность по сравнению с размерами поперечного сечения) и не зависит от физических свойств материала. Поэтому он будет справедлив и для балки, обладающей свойствами ползучести. [9]
Наиболее важным следствием закона плоских сечений является закон подобия, который и рассмотрим ниже. [10]
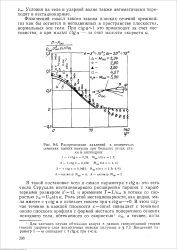 |
Распределение давлений в поперечных. [11] |
Физический смысл такого закона плоских сечений прежний: газ как бы остается в неподвижных в пространстве плоскостях, нормальных оси тела. [12]
Это правило эквивалентно закону плоских сечений и носит название нестационарной аналогии. Эти случаи будут рассмотрены ниже ( см. гл. [13]
В соответствии с законом плоских сечений этому движению эквивалентно обтекание тонкой затупленной впереди пластины ( при v 1) или цилиндра с тупым торцом ( при v - 2); энергия, выделяющаяся при взрыве, эквивалентна сопротивлению затупленного переднего конца пластины или цилиндра. [14]
 |
К теории полос. Особые полосы заштрихо - Тогда из соотношений на ваны скачке уплотнения получим. [15] |
Страницы: 1 2 3 4