Закон - плоское сечение
Cтраница 2
Условие 8С1 приводит к закону плоских сечений и к закону подобия, уже рассмотренным в предыдущей главе. Но условие eiCl дает дополнительные возможности, которые и рассмотрим ниже. [16]
Условие (9.4.11) приводит к закону плоских сечений или нестационарной аналогии. [17]
Мы переходим к некоторым приложениям закона плоских сечений, к задачам, встречающимся в технике. [18]
Во всех движениях рассматриваемого типа справедлив закон плоских сечений [62], который демонстрируется на примере аэродинамики больших скоростей. [19]
Приведенные результаты указывают на возможность использования закона плоских сечений для изучения обтекания потоком с большой сверхзвуковой скоростью тонких, затупленных впереди тел. [20]
 |
Распределение давления. [21] |
Эта особенность гиперзвуковых течений получила название закона плоских сечений, с помощью которого нетрудно определить лобовое сопротивление тела, равное работе расширения соответствующей формы эквивалентного поршня, совершаемой над газом в слое за время прохождения тела сквозь этот слой. [22]
Разумеется, указанное правило, называемое законом плоских сечений, непосредственно следует из приведенных выше оценок, где было показано, что при большой скорости обтекания относительное продольное смещение частиц газа - малая более высокого порядка по сравнению с поперечными смещениями. [23]
Экспериментально установлено, что при упругопла-стическом изгибе закон плоских сечений сохраняется. Поэтому деформации линейно зависят от координаты у. [24]
Это позволяет в рамках приближенных теорий ( закон плоских сечений или нестационарной аналогии) сводить задачу трехмерного ( в общем случае) стационарного обтекания тонкого тела к двумерной нестационарной. Эти идеи были положены в основу создания метода искривленных тел в задачах о нестационарном обтекании тонких тел гиперзвуковом потоком. Метод искривленных тел заключается в замене нестационарного обтекания какого-либо тела стационарным обтеканием другого тела, полученного из первоначального соответствующим искривлением его формы. В дальнейшем этот метод распространен на случай обтекания тонких тел под большими углами атаки, предложен метод расчета нестационарных аэродинамических характеристик с учетом реальных свойств воздуха и произвольных форм носка. [25]
Весной 1947 г. я сформулировал и доказал закон плоских сечений в аэродинамике больших сверхзвуковых скоростей, приводящий пространственную задачу к плоской, а для экспериментаторов давший метод афинной модели. Этот закон казался некоторым настолько неестественным, что специально собравшаяся комиссия, состоявшая из бывшего тогда проректором МГУ всемирно известного математика И.М. Виноградова, М.В. Келдыша и моего оппонента Л. И. Седова, убеждала меня, что этого закона не может быть ( впрочем, И.М. Виноградов молчал, М.В. Келдыш не спешил с выводом); Л.И. Седов же утверждал, что ввиду существования лобового сопротивления этот закон прямо противоречит закону сохранения импульса для системы тело-воздух. В 1947 г. в НИИ-88 закон сразу был использован для экспериментально-теоретического определения сверхзвуковых аэродинамических коэффициентов: была построена теория панельного фляттера, вскоре закон был принят в ЦАГИ как ничему не противоречащий. [26]
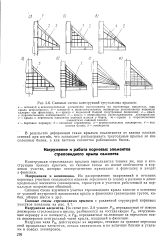 |
Силовые схемы конструкций треугольных крыльев. [27] |
В результате деформации таких крыльев отклоняются от закона плоских сечений при изгибе, что заставляет рассматривать треугольные крылья не как сплошные балки, а как системы совместно работающих балок. [28]
Тем самым показано, что при условиях (9.2.2) закон плоских сечений справедлив и для нестационарного обтекания тонких тел. [29]
При этом возникнут продольные перемещения, распределенные по закону плоских сечений, причем в центре тяжести сечения каждого составляющего стержня эти перемещения будут равны нулю. Получим напряженное состояние, соответствующее изгибу стержня в направлении оси х, которое полностью соответствует поведению составного стержня с абсолютно жесткими поперечными связями при изгибе в главной плоскости инерции полного сечения. [30]
Страницы: 1 2 3 4