Закон - плоское сечение
Cтраница 3
В процессе деформирования поперечные сечения стержня остаются плоскими и справедлив закон плоских сечений. [31]
При сильных ударных волнах и е С 1 имеют место закон плоских сечений и нестационарная аналогия между стационарным гиперзвуковым обтеканием удлиненных двумерных ( пространственных) тел и нестационарным расширением одномерного ( двумерного) поршня. Важно, что в этих условиях указанная аналогия обеспечивает не только качественное, но и количественное соответствие течений. Благодаря этому и перечисленным выше особенностям течений с сильными ударными волнами, удается без использования вычислительных машин получить решение интересных в теоретическом отношении и важных для приложений задач гиперзвукового обтекания. Полученные при этом теоретические результаты оказались близки к экспериментальным данным. [32]
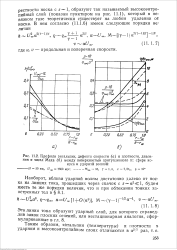 |
Профили энтальпии, дефекта скорости ( а и плотности, давления и чисел Маха ( б между поверхностью притупленного пс сфере конуса, и ударной волной. [33] |
Эти линии тока образуют ударный слой, для которого справедлив закон плоских сечений, или нестационарная аналогия, сформулированные в гл. [34]
Эти формулы выражают так называемый закон секториальных площадей, аналогичный закону плоских сечений, применяемому при изучении изгиба балок. [35]
Эквивалентность трехмерного гиперзвукового обтекания тонких тел плоскому неустановившемуся течению называется иногда законом плоских сечений в гиперзвуковой аэродинамике. [36]
Работа тонкостенных стержней открытого профиля в общем случае не может быть описана законом плоских сечений. Этот закон заменяется более сложным. [37]
В работе [1] на основе факта, что к крыльям предельно малого удлинения приложим закон плоских сечений, сводящий пространственную задачу вихревого обтекания к задаче двумерного нестационарного обтекания пластины, были выведены законы подобия. [38]
Если перед летящим телом выделить слой газа, перпендикулярный направлению скорости тела, то, согласно закону плоских сечений, при движении тела через этот слой в нем образуется ударная волна, за которой частицы газа будут двигаться, не смещаясь в продольном направлении. [39]
Эта формула приближенная, так как она основана на предположении, что осевые перемещения w складываются из перемещений, определяемых законом плоских сечений и законом секториальных площадей. [40]
Вместе с граничным условием (21.21) и условиями (21.13), (21.14) и (21.22) на фронте волны система уравнений (21.34) и (21.37) доказывает закон плоских сечений при установившемся движении. [41]
Расчет трубопровода как балки кольцевого сечения на неосесимметричные нагрузки не отвечает действительному напряженному состоянию трубопровода, так как при действии на него неосесимметричной нагрузки закон плоских сечений теряет силу. При действии неосесимметричных нагрузок ( внутренние отложения пыли, конденсат, ветровая нагрузка, обледенение и т.п.) трубопроводы, имеющие обычно вид тонких оболочек, работают не как плоские конструкции, а как пространственные системы ( оболочка с жесткими опорными кольцами), находящиеся в условиях двухосного напряженного состояния. На действие этих нагрузок трубопроводы рассчитывают как оболочки на основе гипотез технической ( полубезмоментной) теории оболочек. [42]
Считается, что работа каждого отдельного стержня, входящего в составной стержень, протекает в соответствии с обычными законами сопротивления материалов и, в частности, с законом плоских сечений. Поэтому внутреннее напряженное состояние каждого стержня считается полностью определенным, если известны значения моментов, нормальных и поперечных сил в каждом поперечном сечении. Прогибы стержней считаются малыми по сравнению с их длиной, так что в геометрической части задача решается линейными уравнениями, а для стержня имеет место закон независимости действия сил. Исключением, как и для монолитных стержней, являются задачи устойчивости. [43]
Основная идея метода была изложена Г. Г. Черным ( 1956) применительно к гиперзвуковому стационарному обтеканию профилей и тел вращения и к одномерным нестационарным течениям газа, которые в силу закона плоских сечений также могут служить для приближенного описания типерзвукового обтекания тел. Теория сильно уплотненного пограничного слоя, называемая также рядом авторов теорией ударного слоя, за десятилетие, прошедшее со времени опубликования посвященных ей: первых работ, интенсивно развивалась и явилась основным средством аналитического исследования и источником получения результатов о гиперзвуковых течениях невязкого газа около тел. [44]
Для таких тел область течения может быть разделена, как это делал В. В. Сычев, на внутренний слой, в котором плотность газа мала, и внешний возмущенный поток, в котором можно считать выполненным закон плоских сечений. [45]
Страницы: 1 2 3 4