Политоп

Cтраница 1

Политопы, проекции которых служат решениями задачи о размещении треугольников, принадлежат к классу так называемых политопов Гесса. [1]

Политопы невозможно нарисовать на бумаге. Но и 3-мерные фигуры тоже невозможно нарисовать на бумаге. При изображении 3-мерных объектов на плоском листе мы пользуемся определенными соглашениями, которые обусловлены анатомическим строением нашего глаза. [2]

Политоп этого вида часто называется полиматроидным политопом, или, коротко, полиматроидом. [3]

Политопы некоторых типов заслуживают особого внимания. Например, для d О, 1, 2 и 3 соответствующий симплекс является точкой, ребром, треугольником и треугольной пирамидой. Заметим, что треугольная пирамида ( 3-грань в соответствии с принятым соглашением) содержит одну 3-грань ( сама пирамида), четыре 2-грани ( треугольники), шесть 1-граней ( ребра), четыре 0-граней ( вершины) и одну ( - 1) - грань ( пустое множество), что вместе составляет 16 24 граней. [4]

Политоп паросочетаний задается как выпуклая оболочка некоторого множества. Теорема 7.3.1 выдает нам перечень неравенств, необходимых для решения этой задачи, поэтому возникает соблазн попытаться применить эту теорему для конструирования алгоритма построения паросочетаний. [5]

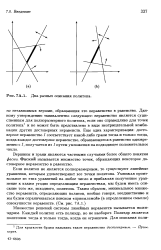А. 1. Два разных описания политопа. [6]

Если политоп не является полноразмерным, то существуют линейные уравнения, которым удовлетворяют все точки политопа. Умножая произвольное из этих уравнений на любое число и прибавляя полученное уравнение к каким угодно определяющим неравенствам, мы будем иметь описание того же, исходного, политопа. [7]

Изменение политопа Р, вызванное добавлением новой точки, можно осуществить не единственным способом. Хотя предлагаемый ниже подход допускает некоторые улучшения на уровне алгоритма, зато он довольно прост для описания. [8]

Поскольку этот политоп определен в терминах неравенств, то, чтобы дать его хорошую характеризацию, нужно описать его вершины. [9]

Комбинаторной природе политопов, и в частности взаимосвязи между числом граней и размерностью, было уделено значительное внимание. [10]

Для каждого политопа существует единственное минимальное множество определяющих его точек, это множество его вершин. [11]

Произвольная вершина политопа, описываемого системой (7.1.7), должна удовлетворять пяти неравенствам с линейно независимыми левыми частями, обращая их в равенства. Она, конечно, должна удовлетворять и остальным неравенствам. Предположим, например, что рассматривается вершина, обращающая в равенства первые четыре неравенства, стоящие в левой части системы (7.1.7), и последнее неравенство из ее правой части. [12]

Нахождение размерности политопа эквивалентно построению линейного базиса для всех тех уравнений, которым удовлетворяют все точки политопа. [13]

Иллюстрация случаев, рассматриваемых в теореме. [14]

Адекватное описание текущего политопа Р дает его граф граней Н ( Р) ( т.е. диаграмма Хассе для множества граней политопа Р, основанная на отношении включения; см. разд. [15]

Страницы: 1 2 3 4