Политоп

Cтраница 2

Напомним, что политоп паросочетаний M ( G) графа G определяется как выпуклая оболочка векторов инцидентности всех паросочетаний графа G. Обратное утверждение также справедливо: каждое приводимое ниже неравенство определяет некоторую грань политопа. [16]

Множество крайних точек политопа X, определяемого ограничениями (11.2), (11.3), соответствует множеству допустимых базисных решений системы (11.2), и при этом одному базисному решению соответствует одна крайняя точка. [17]

Теорема Эдмондса о политопе паросочетаний подсказывает следующую общую задачу. Довольно часто систему неравенств, целочисленные решения которой являются как раз векторами из S, найти несложно. Например, если 5 есть множество векторов инцидентности совокупности паросочетаний, то неравенства (7.1.5), определяющие политоп дробных паросочетаний, имеют в качестве целочисленных решений только паросочетания. [18]

Предположим, что каждый политоп Р из К. [19]

Симплициальным называется d - политоп, каждая гипергрань которого является симплексом. Это эквивалентно тому, что каждая грань симплициального cf - политопа содержит в точности d подграней. С другой стороны ( можно было бы сказать двойственной), d - политоп называется простым, если каждая из его вершин инцидентна в точности d ребрам. В самом деле, легко понять, что симплициальный политоп является двойственным по отношению к простому политопу при понимании двойственности, как это принято в общей топологии, как отображения, отображающего множество размерности s d в множество размерности d - s ( обратите также внимание на более специальное отношение двойственности, воплощаемое полярными преобразованиями, рассмотренными в разд. Симплициальные и простые политопы являются чрезвычайно важными не только из-за их структурной привлекательности и - простите за игру слов - простоты, но также ввиду того, что они естественным образом возникают в двух типичных ( и двойственных. [20]

В случае, когда результирующий политоп является симплици-альным, последнее уравнение имеет единственное решение. [21]

Три п 16 получаются жидкие политопы; при п 16 - пластичные полимеры; при ч - 60, 90, 100 - твердые воскоподоб1 [ ые полимеры. [22]

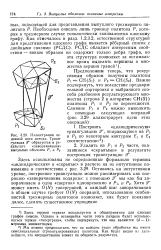Иллюстрация основной идеи метода. Триангуляция Э - образуется в результате заворачивания выпуклых оболочек Р и Р %. [23]

Необходимо описать лишь границу политопа Р, которая в трехмерном случае топологически эквивалентна плоскому графу. Как отмечалось в разд. [24]

Триангуляция ( разбиение) га-мерного политопа, изображающего диаграмму состава, является первым шагом при теоретическом изучении многокомпонентных систем. Путем триангуляции выводятся элементы сингулярной звезды ( отражающие комбинацию солей, не реагирующих между собой - продукты обмена) и неравновесной звезды ( исходные химические вещества, реагирующие между собой с образованием солей сингулярной звезды), а также элементы конверсии, отображающие реакции обмена. [25]

Триангуляция ( разбиение) ге-мериого политопа, изображающего диаграмму состава, является первым шагом при теоретическом изучении многокомпонентных систем. Путем триангуляции выводятся элементы сингулярной звезды ( отражающие комбинацию солей, не реагирующих между собой - продукты обмена) и неравновесной звезды ( исходные химические вещества, реагирующие между собой с образованием солей сингулярной звезды), а также элементы конверсии, отображающие реакции обмена. [26]

Однако в отличие от политопа паросочетаний политоп совершенных паросочетаний не является полноразмерным; поэтому его описание с помощью минимального множества неравенств не единственно. Тем не менее одно из подходящих описаний может быть получено следующим естественным способом. У ( С) - разрез) графа G представляет собой множество ребер, соединяющих подмножество вершин S с подмножеством вершин V ( G ] - S, причем мощности обоих этих подмножеств нечетные. Подмножества S и V ( G) - S называются берегами данного разреза. [27]

Мы также видели, что политопы в случае большого числа измерений уже не являются такими простыми геометрическими объектами, как их двумерные аналоги - выпуклые многоугольники. [28]

Проекция девяти-вершинного политопа пятерной взаимной системы Na, Rb, Tl I Cl, N03, S04 [ TABLE ] 12. [29]

На рис. III.8 дана проекция политопа с нанесенными стабильными диагоналями и индексами вершин, подтверждающими принадлежность взаимной системы Na, Rb, Tl Cl, N03, S04 к типу В. В табл. III.12 выведены индексы вершин стабильных диагоналей и подсчитаны суммы индексов. [30]

Страницы: 1 2 3 4