Последовательность - коэффициент
Cтраница 1
Последовательность коэффициентов имеет одну перемену знака, следовательно уравнение имеет один действительный положительный корень. Уравнение (2.37) имеет еще один отрицательный корень и пару комплексно-сопряженных корней. Это следует из того, что если в (2.37) Tw заменить на - Тш, в ряду коэффициентов полученного многочлена также будет одна перемена знака. [1]
Поскольку последовательности коэффициентов в степенных разложениях (2.120) линейно независимы, коэффициенты перед каждой степенью и перед их смешанными произведениями должны равняться нулю. [2]
Приведенная выше последовательность коэффициентов перед числами верхнего ряда, встречающимися в треугольнике ( 6, 20, 34, 34, 20, 6), совпадает с уменьшенными на единицу числами, образующими седьмую строку треугольника Паскаля. [3]
Qncn) есть последовательность коэффициентов Фурье некоторой меры. [4]
Предполагая, что последовательность коэффициентов сп ( t) остается ограниченной при каждом t, В. Более того, в этом случае ни у одной из двух наших систем нет других решений, и поэтому эти системы по существу эквивалентны. [5]
Вейерштрасса о существовании последовательности коэффициентов степенного ряда, сколь угодно точно приближающего произвольную непрерывную функцию. [6]
Последовательность уп представляет собой последовательность коэффициентов Фурье некоторой меры F на окружности в том и только том случае, когда она положительно определена. [7]
Соотношениями (6.34) и (6.35) последовательность коэффициентов un ( i) определяется однозначно. [8]
Убедитесь в том, что последовательность коэффициентов Yx ( m) получается такой же при использовании алгоритма типа Кули - Тьюки. [9]
Система линейных уравнений (3.22) содержит две последовательности коэффициентов А и Вп. [10]
Решение системы уравнений ( 4) дает последовательность коэффициентов Vi для каждой функции. Эти коэффициенты могли бы быть непосредственно использованы при классификации. Однако их трудно интерпретировать, соответствующие им значения дискриминантной функции не имеют определенного смысла. Причина заключается в том, что данное решение не имеет ограничения по метрике дискриминантного пространства. Хотя это пространство вводится для обеспечения максимального разделения классов, последние могут располагаться в любой его области. [11]
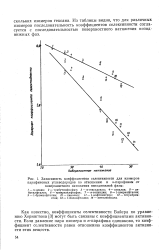 |
Зависимость коэффициентов селективности для изомеров. [12] |
Из таблицы видно, что для различных изомеров последовательность коэффициентов селективности согласуется с последовательностью поверхностного натяжения неподвижных фаз. [13]
Алгоритмы БПФ, в которых на уменьшающиеся последовательности разлагается последовательность коэффициентов S ( k) дискретного преобразования Фурье, называют алгоритмами БПФ с прореживанием по частоте. [14]
Число положительных действительных корней меньше или равно числу перемен знаков в последовательности коэффициентов я0, i, ап. Заменяя х на - х в уравнении (5.5), таким же способом можно оценить число отрицательных корней. [15]
Страницы: 1 2 3 4