Последовательность - коэффициент
Cтраница 4
Такое положение является типичным, но не обязательным. Некоторые из внутригрупповых структурных коэффициентов могут быть больше или меньше, или иметь противоположный знак по сравнению со структурными коэффициентами. Кроме того, они могут иметь различный порядок расположения. Эти две последовательности коэффициентов относятся к разным сторонам структуры данных. [46]
 |
Компьютерная система сбора данных. [47] |
По этим рассчитанным коэффициентам разрабатывается программируемый усилитель, управляемый ТУ-разрядным счетчиком через соответствующий дешифратор. Управляющий сигнал представляет собой периодическую последовательность из N кодов. Для работы счетчика требуется генератор тактовых импульсов. В случае непериодического сигнала процедура проектирования остается той же самой, только последовательность N коэффициентов усиления формируется один раз. Для этого генератор тактовых импульсов посылает на счетчик серию из N синхроимпульсов. [48]
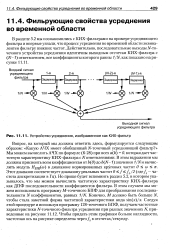 |
Устройство усреднения, изображенное как КИХ-фильтр. [49] |
Вопрос, на который мы должны ответить здесь, формулируется следующим образом: Какую АЧХ имеет обобщенный N-точечный усредняющий фильтр. Мы можем вычислить АЧХ по формуле ( 6 - 28) при всех a ( k) 0, которая дает частотную характеристику КИХ-фильтра с N ответвлениями. В этом случаем мы можем использовать программу М - точечного БПФ для преобразования последовательности N коэффициентов, равных 1 / N. Следуя этой процедуре и используя программу 128-точечного БПФ, получаем частотные характеристики ЛГ-точечного фильтра усреднения при разных значениях N, приведенные на рисунке 11.12. Чтобы придать этим графикам больше наглядности, частотная ось на рисунке определена через / s в отсчетах / секунду. [50]
Ортонормированная система называется полной, если не существует функции единичной энергии, не принадлежащей базису vi ( t), которая бы была ортогональна ко всем функциям базиса. Если хотя бы одна такая функция найдется, то система неполная. Разложение по полной системе ортогональных функций называется обобщенным рядом Фурье. Полные системы позволяют при выборе базиса достаточно большой размерности М отображать с любой заданной точностью все реализации случайного процесса ограниченной энергии в виде последовательностей коэффициентов разложения. [51]
Очевидно, что погрешность приближения к У может стремиться к нулю при п - с лишь тогда, когда (7.10) является равенством. Тогда говорим, что элемент Y принадлежит пространству ( замыканию линейной оболочки) системы (7.1), а равенство называется уравнением замкнутости. Система элементов (7.1) называется замкнутой в Нт, если для любого элемента У из Нт выполняется уравнение замкнутости. Система (7.1) называется полной в том же пространстве, если в нем нет элемента, кроме нулевого, который был бы ортогонален ко всем элементам этой системы. Можно показать, что если система (7.1) замкнута, то она и полна, и если она полна, то и замкнута. I, можно доказать, что для того чтобы последовательность чисел Ai была последовательностью коэффициентов Фурье для какого-либо элемента Y из Нт, достаточно, чтобы форма (7.9) была ограниченной при я - оо. [52]
Первый класс первой группы был рассмотрен в предыдущих параграфах, причем оказалось, что индивидуальные свойства очень сильно зависят. Взаимодействия специфического характера, которые вызывают обращение последовательности коэффициентов активности для катионов в присутствии ионов фтора и гидроксила, согласно Скэтчарду и Прен-тису, также обусловлены очень малыми размерами этих ионов. Хотя точные экспериментальные данные для фторидов почти совершенно отсутствуют, все же можно полагать, что ион фтора является акцептором протонов, так как осмотический коэффициент 1 М раствора фтористоводородной кислоты почти такой же, как осмотический коэффициент муравьиной кислоты при той же концентрации. Если это допущение правильно, то механизм взаимодействия катионов с растворителем ( водой), рассмотренный в § 5, может иметь существенное значение. В анионе большого размера, вроде ацетат-иона, заряд расположен, невидимому, на значительном расстоянии от центра иона. С этим обстоятельством может быть связана способность этих анионов соединяться о протонами и явление обращения последовательности коэффициентов активности для различных катионов. [53]
Первый класс первой группы был рассмотрен в предыдущих параграфах, причем оказалось, что индивидуальные свойства очень сильно зависят от размера ионов. Взаимодействия специфического характера, которые вызывают обращение последовательности коэффициентов активности для катионов в присутствии ионов фтора и гидроксила, согласно Скэтчарду и Прен-тису, также обусловлены очень малыми размерами этих ионов. Хотя точные экспериментальные данные для фторидов почти совершенно отсутствуют, все же можно полагать, что ион фтора является акцептором протонов, так как осмотический коэффициент 1 М раствора фтористоводородной кислоты почти такой же, как осмотический коэффициент муравьиной кислоты при той же концентрации. Если это допущение правильно, то механизм взаимодействия катионов с растворителем ( водой), рассмотренный в § 5, может иметь существенное значение. В анионе большого размера, вроде ацетат-иона, заряд расположен, повидимому, на значительном расстоянии от центра иона. С этим обстоятельством может быть связана способность этих анионов соединяться с протонами и явление обращения последовательности коэффициентов активности для различных катионов. [54]
Страницы: 1 2 3 4