Самосогласованный потенциал

Cтраница 1

Самосогласованные потенциалы / - ( г) в общем случае не являются центрально-симметрическими. [1]

Группирование уровней самосогласованного потенциала в оболочки. [2]

Атомный самосогласованный потенциал на малых расстояниях от ядра имеет вид кулоновского, а вдали от ядра стремится к нулю быстрее кулоновского за счет экранирования ядерного потенциала электронным облаком. [3]

Безразмерный самосогласованный потенциал GaA ( r) расходится в нуле в случае кулоновского потенциала. Поэтому обычно производилось обрезывание кулоновского потенциала. Не останавливаясь на законности и преимуществах такого обрезывания, предположим до § 4, что функция GaA ( r) при г 0 не имеют особенностей. [4]

Предполагая, что осцилляторный характер самосогласованного потенциала сохраняется и для тяжелых ядер Лз 1, на основе квазиклассическнл соображений получить выражение для плотности нуклонов в таких ядрах. [5]

Пусть F ( r) - самосогласованный потенциал для электрона с учетом как поля ядра, так и среднего поля, образуемого другими электронами вакуумной оболочки. [6]

Псевдопотенциалы в одноатомном одномерном кристалле. а - истиный. б t - модельный. [7]

Пусть V ( г) есть самосогласованный потенциал, действующий на отдельный электрон. [8]

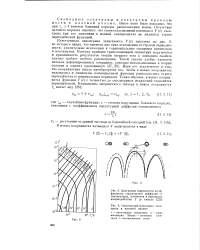Диаграмма зависимости коэффициента структурной диффузии от температуры, плотности и параметра взаимодействия Г ( в смысле.| Одномерный потенциал электрона в плотной плазме. [9]

Отсутствие дальнего порядка означает, что самосогласованный потенциал V ( г) электрона при его движении в ионной квазирешетке не является строго периодической функцией. [10]

Большая же часть горячих электронов захвачена самосогласованным потенциалом. [11]

К каким значениям магических чисел приводит такая модель самосогласованного потенциала. [12]

В зависимости от выбора нулевого приближения при построении самосогласованного потенциала различают два метода решения уравнений Хартри ( Фока): метод слабо связанных электронов и метод сильно связанных электронов. [13]

Для каждой суперконфигурации Н средняя энергия вычисляется в своем самосогласованном потенциале, соответствующем числам заполнения одной из конфигураций, либо средней конфигурации. [14]

Это сильно отличается от вычисления Флори для одиночной цепи, где самосогласованный потенциал локализован в малой области пространства и воздает конечную силу, действующую на цепь. [15]

Страницы: 1 2 3 4