Принцип - вольтерр
Cтраница 3
Исследования в области плоских и пространственных контактных задач вязкоупругости показали, что в случае монотонного возрастания области контакта принцип Вольтерра дает правильное решение. [31]
Третий из указанных случаев a ( t) l ( t) аналогичен предыдущему и для него справедливы критерии применимости принципа Вольтерра, изложенные выше. [32]
К этому выводу можно прийти, основываясь на результатах работы [127], в которой с общих позиций строго обоснованы критерии применимости принципа Вольтерра для ряда задач теории вязкоупругости с изменяющимися со временем граничными условиями. [33]
Он выписал решение задачи для трещины, ослабляющей тонкую упругую пластинку, где к берегам разреза приложены равные по величине сосредоточенные силы, и, воспользовавшись принципом Вольтерра, получил уравнение движения концов трещины разрушения, заменив модуль Юнга соответствующим временным оператором. [34]
Как следует из (7.11), условие плавности смыкания берегов трещины совпадает с условием конечности напряжений (7.10) только в случае коммутативности операций интегрирования и действия оператора Г, что эквивалентно принципу Вольтерра. [35]
Из условия (7.12) следует, что при однородном растяжении плоскости усилиями 7о ( t) po const размер концевой зоны растет, если растет l ( t), следовательно, в этом случае справедливо применение принципа Вольтерра. [36]
Заметим, что вариационные принципы наследственной теории упругости допускают и иную трактовку. Вследствие принципа Вольтерра можно применять любой метод для решения задачи обычной теории упругости, и лишь в окончательном результате упругие константы следует заменить операторами. Отсюда следует, в частности, что для нахождения точного или приближенного решения задачи теории упругости может быть применен любой из известных вариационных методов; если в результате решения в окончательном результате появится некоторая комбинация упругих констант, ее можно заменить такой же комбинацией из операторов и расшифровать по известным правилам. [37]
Значит, согласно принципу Вольтерра 3), в наследственно-упругом теле напряжения будут такими же, как в упругом. [38]
Поэтому, чтобы получить решение задачи наследственной теории упругости, нужно сначала построить решение обычной задачи и В окончательных результатах заменить упругие постоянные операторами, расшифровав полученные комбинации операторов по известным правилам. Основное ограничение для применения принципа Вольтерра состоит в том, чтобы вид граничных условий сохранялся неизменным. [39]
Отметим, что точно такое же соотношение можно получить с помощью принципа Вольтерра. Таким образом, в рассмотренном случае принцип Вольтерра справедлив при любом характере изменения длины трещины. [40]
Применяя преобразование Лапласа к системе уравнений и граничных условий задачи вязкоупругости, для изображений получают уравнения классической теории упругости; после решения этой задачи уже в окончательном результате переходят от изображений к оригиналам. Ограничения, отмеченные выше в связи с применением принципа Вольтерра, сохраняют силу и в этом случае. Основная трудность состоит в фактическом выполнении обращения Мел-лина. [41]
Это обстоятельство используется при решении квазистатических краевых задач вязкоупругости с помощью принципа Вольтерра. [42]
Следует отметить, что работе [62] предшествовали исследования [29, 40, 41] близких к рассматриваемой проблеме задач контактного взаимодействия вязко-упругих тел. В монографии [141] указан круг задач механики разрушения, где следует применять принцип Вольтерра. В этой работе на основе принципа Вольтерра получено распределение деформаций и напряжений у края трещины в вязко-упругом теле. В работе [72] определено напряженно-деформируемое состояние в вязко-упругой композитной пластине с трещиной, расположенной вдоль одной из осей упругой симметрии композиционного материала. [43]
В сороковые - пятидесятые годы, когда наследственная теория упругости получила новое развитие в работах американских авторов, для решения задач получил широкое распространение метод, основанный на применении преобразования Лапласа. Для этого метода был сформулирован принцип соответствия, который по существу представляет собою простую перефразировку принципа Вольтерра. [44]
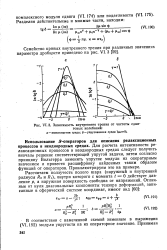 |
Зависимость внутреннего трения от частоты сдвиговых колебаний. а - вязкоупругая среда. б - упруговязкая среда ( цо0. [45] |
Страницы: 1 2 3 4