Ветвящийся процесс
Cтраница 1
 |
Примеры циклических алгоритмов. [1] |
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей - сложным. [2]
Ветвящийся процесс с конечным числом типов частиц может служить моделью при расчетах цепных реакций; ветвящийся процесс с диффузией частиц - моделью нейтронных процессов в ядерных реакторах. [3]
Ветвящийся процесс - это процесс размножения и превращения частиц, в котором частицы развиваются независимо друг от друга. [4]
Ветвящиеся процессы с а 1, а - 1 и а 1 называют соответственно докритическими, критическими ( если ( f ( x) x) и надкритическими. Асимптотические свойства ветвящихся процессов в этих трех случаях существенно различны. [5]
Общий ветвящийся процесс в пространстве позволяет вычислять корреляторы путем дифференцирования формул (111.50), ( III. [6]
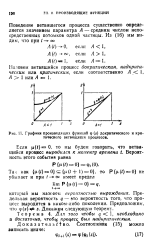 |
Графики производящих функций р ( s докритнческого и критического ветвящихся процессов. [7] |
Поведение ветвящегося процесса существенно определяется значением параметра А - средним числом непосредственных потомков одной частицы. [8]
Переход ветвящихся процессов в диффузионные и примыкающие задачи генетики. Резюме доклада на заседании семинара кафедры теории вероятностей Московского университета, 18 ноября 1958 г. ] / / Теория вероятн. [9]
Переход ветвящихся процессов в диффузионные и примыкающие задачи генетики ( обзорный доклад) ( перепеч. [10]
Теория ветвящихся процессов дает выражение и для макромолекул средних размеров. [11]
Теория ветвящихся процессов с частицами нескольких типов аналогична, но более сложна. [12]
Мы рассматривали ветвящийся процесс, начинающийся с одной частицы. [13]
При исследовании ветвящихся процессов часто используются производящие функции. [14]
Во-вторых, многие ветвящиеся процессы протекают очень быстро, и разбиение их даже на малые дискретные участки приводит к большим погрешностям - так интенсивно меняются характеристики процесса на протяжении этих промежутков. Поэтому считают процесс непрерывным и полагают, что время от одного перехода до другого является величиной случайной, имеющей определенные вероятностные характеристики. При этом мы снова имеем дело с математической моделью в виде дифференциальных уравнений Колмогорова - Чепмена, о которых уже говорилось выше. [15]
Страницы: 1 2 3 4