Микроскопический процесс

Cтраница 2

Физическая постоянная, входящая в выражение законов, описывающих микроскопические процессы; численно равна 6 62 - Ю Джс. [16]

Елок, которое может появиться в уравнениях, описывающих микроскопические процессы. Вывод, представленный здесь для изотропной среды, может быть распространен на анизотропные среды. [17]

В неравновесной статистической механике кинетические коэффициенты получают путем рассмотрения микроскопических процессов рассеяния. Такой подход впервые был реализован с помощью уравнения Больцмана, которое справедливо для систем с короткодействующим взаимодействием в предельном случае низкой плотности. Мы приведем некоторые частные результаты для проводимости а, часто встречающиеся в литературе [ [109, 436, 480, 601]; эти формулы для проводимости можно вывести, пользуясь единым подходом в рамках изложенной ниже теории линейного отклика. [18]

Зависимость локального повышения температуры от времени после разрыва стального образца ( разрыв происходит в течение 2 мксек при одноосном растяжении. Показан образец и места расположения на нем термопар. Номера кривых соответствуют номерам термопар. [19]

Следовательно, достаточно упругие стекла могут разрушаться за счет микроскопических процессов пластической деформации, поскольку вязкоупругая составляющая деформации может увеличиться в области какой-либо негомогенности, являющейся концентратором напряжения, а значение напряжения здесь может на порядок превосходить номинальное. [20]

Ел ж, которое может появиться в уравнениях, описывающих микроскопические процессы. Вывод, представленный здесь для изотропной среды, может быть распространен на анизотропные среды. [21]

Согласно принципу детального равновесия, в равновесной термодинамической системе каждый микроскопический процесс сопровождается обратным ему процессом, причем вероятность обоих процессов одинакова. Основываясь на этом принципе, Эйнштейн постулировал, что вероятность вынужденных переходов, сопровождающихся излучением, должна быть равна вероятности вынужденных переходов, сопровождающихся поглощением света. [22]

Несмотря на свое название, эта книга в основном рассматривает микроскопические процессы мозга и почти не уделяет внимания тому, как из путаницы нейронов возникают человеческие мысли. Особенно подробно прокомментирована работе Хубеля и Визеля о зрительных системах. [23]

Физические воздействия позволяют интенсифицировать не только макроскопические, но и микроскопические процессы атомно-молеку-лярного уровня. Для химической технологии особый интерес представляют специфические ( избирательные) воздействия, приводящие к химическим превращениям веществ, которые невозможны при использовании других методов. [24]

Макроскопическая остаточная деформация растяжения или сжатия поликристаллического твердого тела является результирующей микроскопического процесса дробления кристаллических зерен, при котором сплошность или объем тела практически сохраняются или изменяются крайне мало. Этот необратимый дислокационный процесс, протекающий под действием внешних сил, хорошо наблюдать электронно-микроскопическим или рентгенографическим методами. Важно обратить внимание на то, что в результате исследования деформаций, напряжений и структурных изменений, определяющих свойства металла в процессе деформирования, установлена их взаимосвязь. [25]

Кинетические эффекты в кулоновских системах - это макроскопические явления, определяемые микроскопическими процессами, для описания которых необходима теория многих частиц. [26]

Так как свойства макроскопических тел ( систем) обусловлены протекающими в них микроскопическими процессами беспорядочного движения микрочастиц, то объяснить и количественно охарактеризовать свойства макросистем можно на основе рассмотрения этих микропроцессов. [27]

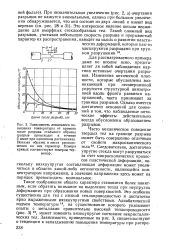
Зависимость вязкости разрушения ( Кс и характера разрушения ( Р от толщины образца, показывающая переход от преимущественного плоско-напряженного к плоско-деформированному состоянию. [28]

Способы определения податливости образцов с трещиной позволяют непосредственно измерять количество энергии, затрачиваемой на микроскопические процессы, протекающие в материале при росте трещины. Рост трещины обычно происходит при двух различных условиях. Во-первых тело подвергается действию постоянной нагрузки, например постоянного веса, а во-вторых, постоянной деформации. Ниже описан принцип определения поверхностной энергии разрушения по податливости образцов с трещиной при условии постоянства деформации. [29]

Здесь мы имеем дело с детальным равновесием в буквальном смысле этого слова: каждый микроскопический процесс столкновений балансируется обратным ему процессом. [30]

Страницы: 1 2 3 4