Латинский прямоугольник
Cтраница 2
Обратно, такой конфигурации У соответствует некоторое непустое множество латинских прямоугольников на Zn размера г У. [16]
 |
Влияние различных концентраций компонентов среды на выход антибиотика. [17] |
Если опыты выполняются тщательно, то с помощью планов ортогональных латинских прямоугольников можно быстро получить ответ на вопрос об оптимальных условиях ведения процесса. Если же кривые эффект - концентрация имеют скачущий характер, то это свидетельствует о том, что результаты опытов недостаточно достоверны. Обычно при этом и абсолютные величины эффектов невелики. [18]
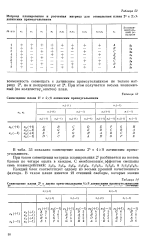 |
Совмещение плана 25 с 4X8 латинским прямоугольником.| Совмещение плана 25 с двумя ортогональными 4Х § латинскими прямоугольниками. [19] |
В табл. 53 показано совмещение плана 25 с 4x8 латинским прямоугольником. [20]
Тесную связь с приведенными задачами имеет проблема определения числа Lkn латинских прямоугольников fcXn и числа Ln латинских квадратов. [21]
В табл. 54 приведен план, построенный на базе двух ортогональных латинских прямоугольников. В табл. 55 приведен индекс сложных совмещенных планов. [22]
В нее включен материал о специальных классах матриц, о латинских прямоугольниках и квадратах, о тройках Штейнера и других видах комбинаторных наборов и о блок-схемах. [23]
Локальная асимптотическая нормальность числа пар отрезков последовательности, связанных подстановками из латинского прямоугольника. [24]
Когда имеешь дело с такими задачами, как, например, перечисление латинских прямоугольников, такое ограничение становится необходимым. [25]
Для оптимизации окисления последовательно применены методы математического планирования экстремальных экспериментов: метод латинских прямоугольников, симплекс-метод и рототабельное планирование. [26]
Предельные теоремы для случайных величин от числа пар отрезков, связанных подстановками из латинского прямоугольника. Третья Всероссийская школа-коллоквиум по стохастическим методам. [27]
 |
Проведение контурно-графического анализа по схеме В. Клеймана. [28] |
Для случая, когда число факторов больше числа уровней каждого фактора, разработаны схемы ортогональных латинских прямоугольников. [29]
Начальная серия опытов ( табл. 2), соответствующая вершинам исходного симплекса, была выбрана на основании результатов планирования методом латинского прямоугольника. [30]
Страницы: 1 2 3 4