Пэтрик
Cтраница 1
Пэтрик и Кемпер указывают, что понижение точки плавления адсорбированного вещества можно легко объяснить по теории капиллярной конденсации. Пользуясь простым термодинамическим рассуждением, можно доказать, что жидкость в растянутом состоянии должна затвердевать при более низкой температуре, чем нормальная жидкость, при условии, что она находится в равновесии с нормальной твердой фазой. [1]
Пэтрик и Грейдер [45] проверили экспериментально правильность уравнения ( 31) для теплоты смачивания силикагеля водой и двуокисью серы. [2]
Пэтрик и Кемпер указывают, что понижение точки плавления адсорбированного вещества можно легко объяснить по теории капиллярной конденсации. Пользуясь простым термодинамическим рассуждением, можно доказать, что жидкость в растянутом состоянии должна затвердевать при более низкой температуре, чем нормальная жидкость, при условии, что она находится в равновесии с нормальной твердой фазой. [3]
Пэтрик и Грейдер [45] проверили экспериментально правильность уравнения ( 31) для теплоты смачивания силикагеля водой и двуокисью серы. [4]
В 1927 г. Фрэзер, Пэтрик и Смит [14] провели важное исследование для установления толщины адсорбированного слоя на гладкой поверхности стекла. [5]
В 1927 г. Фрэзер, Пэтрик и Смит [14] провели важное исследование для згстановления толщины адсорбированного слоя на гладкой поверхности стекла. [6]
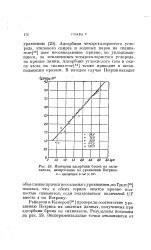 |
Изотермы адсорбции брома на силикагеле, начерченные по уравнению Пэтрика. - адсорбция в х 1 4. [7] |
Райерсон и Камерон [36 ] проверяли соответствие уравнению Пэтрика их опытных данных, полученных при адсорбции брома на силикагеле. [8]
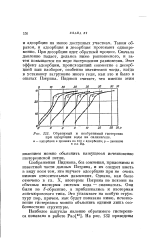 |
Обратимый и необратимый гистерезис. [9] |
Соображения Пиджона, без сомнения, приложимы к известной части данных Пэтрика, и их следует иметь в виду всем тем, кто изучает адсорбцию при не очень низких относительных давлениях. [10]
Выводом из всех изложенных выше рассуждений является то, что уравнение Пэтрика следует рассматривать лишь как эмпирическое уравнение, каким оно и является в действительности. Так как ни уравнение Фрейндлиха, из которого оно было получено, ни введение в него других членов ( р0 и а в дробной степени) не вытекают из какого-либо последовательного разви - ТЕЩ теории капиллярной конденсации, то в том, что экспериментальные данные подчиняются уравнению Пэтрика, нельзя видеть подтверждения теории капиллярной конденсации. Критерием законности эмпирического уравнения являются его успехи в отображении экспериментальных данных. В тех случаях, когда уравнение Пэтрика применимо, оно полезно - как интерполяционная формула. [11]
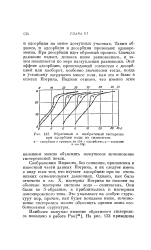 |
Обратимый и необратимый гистерезис. [12] |
Соображения Пиджона, без сомнения, приложимы к известной части данных Пэтрика, и их следует иметь в виду всем тем, кто изучает адсорбцию при не очень низких относительных давлениях. [13]
Выводом из всех изложенных выше рассуждений является то, что уравнение Пэтрика следует рассматривать лишь как эмпирическое уравнение, каким оно и является в действительности. Так как ни уравнение Фрейндлиха, из которого оно было получено, ни введение в него других членов ( р0 и а в дробной степени) не вытекают из какого-либо последовательного развития теории капиллярной конденсации, то в том, что экспериментальные данные подчиняются уравнению Пэтрика, нельзя видеть подтверждения теории капиллярной конденсации. Критерием законности эмпирического уравнения являются его успехи в отображении экспериментальных данных. В тех случаях, когда уравнение Пэтрика применимо, оно полезно как интерполяционная формула. [14]
 |
Образец для измерения пластичности при разрушении клеевого соединения армированных пластикови. [15] |
Страницы: 1 2 3 4