Разбегание - траектория
Cтраница 1
Разбегание траекторий само по себе еще не приводит к стохастич-ному поведению. Необходимо еще существование некоторых статистических закономерностей, наличие средних по времени величин, связанных с тем, что система вновь и вновь возвращается в состояния, близкие к исходным. Такие движения возможны, если в фазовом пространстве имеются незамкнутые траектории, бесконечно и беспорядочно блуждающие внутри некоторой ограниченной области. Подобные траектории образуют инвариантные множества, которые в случае диссипативных систем являются аттракторами. [1]
 |
Эволюция области А в случае перемешивания. [2] |
Разбегание траекторий означает непредсказуемость поведения системы. Если в начальный момент времени положение фазовой точки было известно с конечной точностью, т.е. при t 0 мы знаем лишь, что эта точка принадлежит некоторой области 7е с характерным размером б, то сказать, где именно она окажется через достаточно длительный промежуток времени, невозможно. [3]
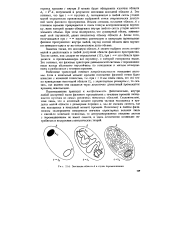
 |
Седловая траектория и близкие к ней. [4] |
Разбегание траекторий сколь угодно далеко невозможно вследствие ограниченности размеров области фазового пространства, в которой допустима эволюция системы. Поэтому траектории со временем изгибаются, и общая картина их оказывается сильно запутанной. Продолжительность времени, в течение которого поведение системы при заданных начальных условиях полностью предсказуемо, очень мала. По истечении времени порядка т начальные условия системой забываются, и состояние системы оказывается не вполне определяемым. Практически т очень мало и даже при возрастании точности задания начальных условий в 105 раз т увеличивается лишь на один порядок. Вследствие неопределенности эволюции для диссипативной системы даже при малом отклонении ее от равновесного состояния нельзя указать аттрактор как конкретное состояние ( точка или предельный цикл), к которому она приближается с течением времени. [5]
 |
Бифуркация Хопфа. [6] |
Разбегание траекторий само по себе еще не приводит к стохас-тичному поведению. Необходимо еще существование некоторых статистических закономерностей, наличие средних по времени величин, связанных с тем, что система вновь и вновь возвращается в состояния, близкие к исходным. [7]
 |
Бифуркация Хопфа. [8] |
Разбегание траекторий само по себе еще не приводит к стохастич-ному поведению. Необходимо еще существование некоторых статистических закономерностей, наличие средних по времени величин, связанных с тем, что система вновь и вновь возвращается в состояния, близкие к исходным. Такие движения возможны, если в фазовом пространстве имеются незамкнутые траектории, бесконечно и беспорядочно блуждающие внутри некоторой ограниченной области. Подобные траектории образуют инвариантные множества, которые в случае диссипативных систем являются аттракторами. [9]
Известное в классической механике экпоненциальное разбегание близких траекторий здесь полностью теряет смысл. [10]
В классическом случае необратимость связана с сильной неустойчивостью системы, т.е. с разбеганием траекторий в фазовом пространстве. А в квантовом случае обращение по времени превращает рассеянные расходящиеся волны в сходящиеся волны. Ясно, что малое внешнее возмущение легко разрушает когерентность сходящихся волн. Поэтому в газе, контактирующем с термостатом, эволюция функции ф ( - 1) должна быть сходна с эволюцией j / ( t): и в том, и в другом случае должны присутствовать рассеянные волны. [11]
С точки зрения не линеаризованной, а исходной динамической системы ляпуновские показатели характеризуют скорость разбегания бесконечно близких траекторий, а показатели высших порядков - скорость изменения бесконечно малых фазовых объемов. [12]
Чтобы продвинуться дальше, нам нужно рассмотреть еще одну особенность хаотических систем, а именно, разбегание траекторий в фазовом пространстве. Из рисунка 13 видно, что близкие вначале траектории экспоненциально быстро разбегаются друг от друга. Именно это разбегание траекторий и приводит в конце концов к необратимости. [13]
Чтобы продвинуться дальше, нам нужно рассмотреть еще одну особенность хаотических систем, а именно, разбегание траекторий в фазовом пространстве. Для этого опять выберем некоторую пробную частицу ( см. рис. 1) и рассмотрим, наряду с ее реальной траекторией, близко расположенную возможную траекторию движения. [14]
На первый взгляд, требование о неустойчивости всех траекторий, принадлежащих аттрактору, и требование о том, чтобы все соседние траектории при t - оо к нему стремились, кажутся несовместимыми, поскольку неустойчивость означает разбегание траекторий. [15]
Страницы: 1 2