Топологическая размерность

Cтраница 2

А вот параллельное существование фрактальной и топологической размерности является самой что ни на есть суровой необходимостью. [16]

Описанный подход к теории топологической размерности нормированных пространств был предложен М. Г. Крейном, М. А. Красносельским и Д. П. Мильманом ( 1948) в качестве основы для исследования таких свойств подпространств, которые устойчивы при малых возмущениях. [17]

Следовательно, все гильбертовы пространства одинаковой топологической размерности изометричны. [18]

Эта величина больше единицы ( топологической размерности линии), но меньше Евклидовой размерности плоскости, d 2, на которой расположена кривая. [19]

Хаусдорфа-Безиковича для которых строго больше его топологической размерности. [20]

Если алгебраическое множество V dRm имеет топологическую размерность нуль ( например, если V состоит лишь из изолированных точек), то V является конечным множеством. [21]

Под размерностью мы понимаем индуктивную или топологическую размерность. [22]

Множества, для которых хаусдорфова размерность строго больше топологической размерности, называются фрактальными множествами, или фракталами. При этом предполагается, что множество принадлежит n - мерному евклидову пространству или многообразию, и диаметр покрывающего множества вычисляется в метрике этого пространства или многообразия. Поэтому определение фрактала требует фиксации метрики. [23]

А ( f) компактно и имеет конечную топологическую размерность. [24]

Одним из важнейших топологических инвариантов является введенная П. С. Урысоном топологическая размерность прострап-пна X ( см. [3], гл. [25]

В математике существует несколько различных определений размерности, наиболее известна топологическая размерность. Идея определения размерности была высказана еще А. Размерность пустого множества полагается равной - 1 и далее по индукции. [26]

Этапы построения плоского регулярного фрактала - салфетки Серпинского. [27]

Кривую Кох можно растянуть в прямую линию, поэтому ее топологическая размерность равна единице. [28]

Кривую Кох можно растянуть в прямую линию, поэтому ее топологическая размерность равна единице. [29]

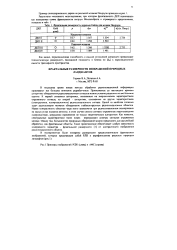Примеры изображений. РЛИ ( слева и АФС ( справа. [30]

Страницы: 1 2 3 4