Распад - произвольный разрыв
Cтраница 1
Распад произвольного разрыва в магнитной гидродинамике, Прикл. [1]
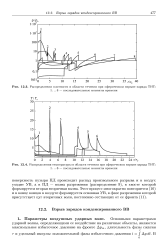 |
Распределения плотности в области течения при сферическом взрыве заряда ТНТ.| Распределения температуры в области течения при сферическом взрыве заряда ТНТ. [2] |
ПД происходит распад произвольного разрыва и в воздух уходит УВ, а в ПД - волна разрежения ( распределение 9), в хвосте которой формируется вторая вторичная волна. [3]
Задача о распаде произвольного разрыва может возникнуть и при более сложных, чем одномерные, пространственных распределениях параметров газа, когда начальная поверхность раздела искривлена и скорость газа с обеих сторон в общем случае имеет все три компоненты, не равные нулю. Для выяснения того, что происходит при распаде такого разрыва, обобщим сначала сформулированную ранее постановку задачи об одномерном разрыве на случай, когда газ с каждой стороны плоской поверхности раздела однороден, но скорость его может иметь все три компоненты не равными нулю. [4]
Решение задачи о распаде произвольного разрыва заключается в отыскании такой совокупности устойчивых разрывов, которая позволяет с помощью условий на них связать значения всех характеристик среды справа и слева от поверхности произвольного разрыва. [5]
Обобщенная задача о распаде произвольного разрыва, Прикл. [6]
Эта задача о распаде произвольного разрыва соответствует вытеснению нефти из водо - и нефтенасыщенного пласта. [7]
Таким образом, при распаде произвольного разрыва возможно образование лишь трех существенно различных волновых конфигураций. [8]
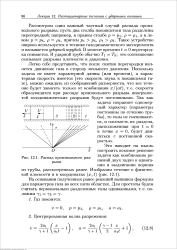 |
Распад произвольного разрыва. [9] |
Рассмотрим один важный частный случай распада произвольного разрыва: пусть два столба покоящегося газа разделены перегородкой; например, в правом столбе р - р, р - р, а в левом р р5 Р Рь, причем pi p i Pi Р5 - Такое устройство широко используется в технике газодинамического эксперимента и называется ударной трубой. В момент времени t 0 перегородка снимается. В ударной трубе обычно 7 Т § это соотношение связывает разрывы плотности и давления. [10]
В общем случае задача о распаде произвольного разрыва решается численно. [11]
Эта задача называется задачей о распаде произвольного разрыва. [12]
В общей постановке задача о распаде произвольного разрыва формулируется следующим образом: в начальный момент t 0 в неограниченном пространстве вдоль плоскости s О все параметры газа испытывают произвольный разрыв. В классической постановке предполагается, что диссипативные процессы в среде отсутствуют. Газ по обе стороны от разрыва в общем случае может обладать разными термодинамическими свойствами, например разными постоянными в уравнениях состояния. [13]
Рассмотрим одномерную задачу о начальном этапе распада произвольного разрыва. Если т - минимальное время релаксации, определяемое слагаемыми f, q, Fn, Fr и Q в (1.5) и (3.2), то задача включает начальный этап 0 t С т, на котором перечисленные слагаемые можно опустить. &, которые находятся в процессе решения, разбивают плоскость xt на зоны разной структуры. Кроме зон постоянных параметров, решение в общем случае содержит центрированные волны с непрерывным изменением параметров от луча к лучу. [14]
Во многих случаях, когда задача о распаде произвольного разрыва имеет неединственное решение, существуют ударные волны, которые, в соответствии с законами сохранения, могут распадаться на систему волн, распространяющихся с различными скоростями. В тех случаях, когда подобная волна существует, именно ее присутствие приводит к неединственности решения задачи Римана. Однако, возможность распада ударной волны, допускаемая законами сохранения, не подразумевает, что ударная волна обязательно распадается и что волны, которые могут распадаться, не существуют. Это обстоятельство отмечалось рядом авторов, в том числе в обзорной работе Кузнецова ( Кузнецов, 1989), посвященной связи устойчивости ударных волн в газе с возможностью их распада. Как хорошо известно, при определенных условиях метастабильные состояния могут существовать длительное время. [15]
Страницы: 1 2 3 4